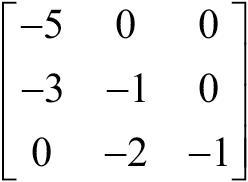행렬의 연산

이러한 행렬 역시 벡터와 동일하게 합과 차, 스칼라의 곱을 구할 수 있다. 벡터의 합과 차, 스칼라의 곱을 다시 떠올려보자. 벡터 간의 합이나 차는 원소의 개수가 같은 두 벡터에서 같은 위치에 대응되는 원소끼리 더하거나 빼고, 계산 결과를 벡터로 정리했었다. 행렬에서의 합과 차도 동일하다. 행과 열의 크기가 같은 두 행렬에서 같은 위치의 원소끼리 더하거나 빼고, 결과를 같은 크기의 행렬에 정리하면 된다.

다음 예처럼 두 행렬의 합을 구해보자. 우선 첫 번째 행렬의 1행 1열의 값인 3과 두 번째 행렬의 1행 1열의 값인 5를 더하여 결과 행렬의 1행 1열에 8을 넣는다. 동일하게 행렬의 모든 값을 이렇게 더하면 된다.

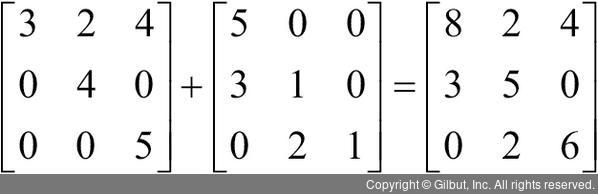
이제는 두 행렬의 차를 살펴보자.

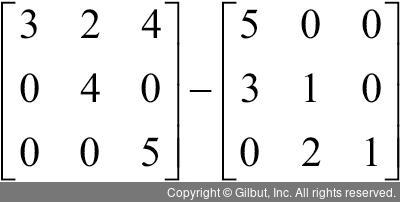
두 행렬의 차를 구하기 전에 우선 뒤에 있는 행렬을 살펴보자. 뒤 행렬은 다음과 같이 다시 쓸 수 있다.

즉, 행렬에 스칼라 -1을 곱한 것이다. 앞에서 스칼라와 벡터의 곱을 다룬 적이 있었는데, 그 경우 스칼라를 벡터의 모든 원소에 곱했다. 스칼라와 행렬의 곱도 같다. 스칼라 -1을 행렬의 모든 원소에 곱하고 그 결과를 행렬로 표현하면 된다. 앞의 스칼라와 행렬을 곱한 결과는 다음과 같다.