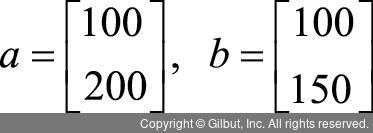그림을 보니 단순한 수치로만 주어졌을 때보다 두 사람의 특성을 직관적으로 이해하고 비교할 수 있다. A와 B 각각에 대해서 점으로 표현하는데 각 점은 몸무게와 키 관점으로, 원점에서 측정된 값만큼 떨어져 있다. 원점이라는 기준이 없다면 공간에 표현할 수 없다. 그렇다면 원점부터 각 점 사이를 연결한 직선으로도 이해할 수 있다. 추가적으로 원점에서 각 점으로 향하는 방향으로 화살표로 표현해보자. 이제부터 이렇게 표현된 각 직선을 벡터라고 부른다.

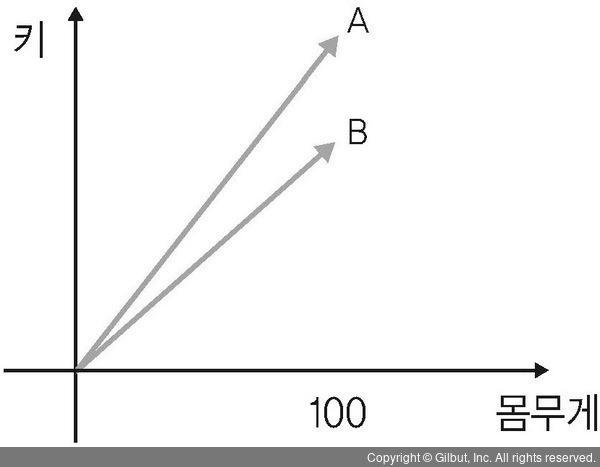
▲ 그림 2-4 키와 몸무게를 표현하는 벡터

그림 2-4에서 볼 수 있듯이, 벡터는 방향과 크기를 갖는 직선으로 이해할 수 있다. 이때 그림처럼 몸무게와 키라는 두 관점, 즉 2차원에서의 직선이 될 수도 있고, 더 많은 차원에서의 직선으로 표현할 수도 있다.

벡터는 좀 더 간단하게 표현할 수 있다. A는 100, 200이라는 값을, B는 100, 150이라는 값을 가지니 다음처럼 나타낼 수 있다. 이렇게 나름의 기준으로 어떤 값의 모음을 한 줄로 표현한 것도 벡터라고 부른다. 일반적으로 벡터는 굵은 알파벳 소문자로 표현하는데, 다음은 A와 B의 키와 몸무게를 나타낸 벡터 a와 b이다. 그리고 벡터를 구성하는 각 값을 원소(element)라고 부르며, 벡터의 각 원소 값은 a_i나 b_i로 표현할 수 있다.