더한 결과 값이 바로 결과 행렬의 1행 1열의 값이 된다. 그리고 이 과정을 행렬의 각 원소에 대해 모두 수행한다. 전체적인 계산 과정은 다음과 같다.

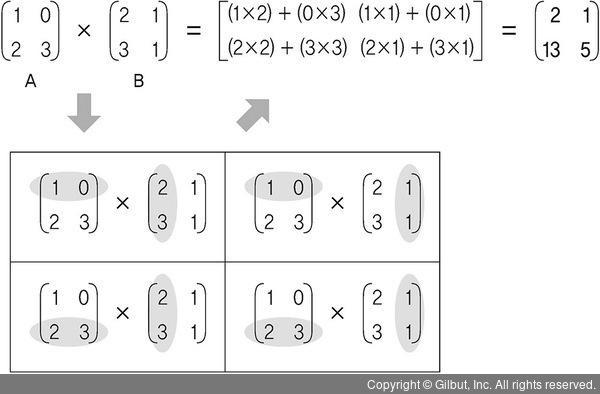
▲ 그림 2-11 행렬 간 곱셈2

이때 바로 벡터 간의 곱셈에서 암기가 필요한 부분은 앞의 벡터는 횡벡터, 뒤의 벡터는 종벡터부터 계산한다는 것이다. 이 방식에 의하면 횡×종의 경우(두 벡터의 원소의 수가 같은 경우), 하나의 숫자가 나오게 되고 이를 내적(inner product)이라 부른다.

만약 두 벡터의 원소의 수가 같은데 앞 벡터는 종벡터이고, 뒤 벡터는 횡벡터이면 어떻게 될까? 우선, 앞 벡터가 종벡터이므로 열의 수는 항상 1이 되고, 뒤 벡터가 횡벡터이므로 행의 수는 항상 1이 된다. 즉, 곱셈은 가능하다. 앞 벡터의 각 행에는 숫자 한 개만 있고, 뒤 벡터의 각 열에도 숫자 한 개만 있게 되며, 두 숫자를 차례대로 곱하면 된다.