다음 예를 보면 앞 벡터 1행 1열인 a와 뒤 벡터 1행 1열인 c를 곱하고, 그 결과는 결과 행렬의 1행 1열이 된 것을 알 수 있다. 앞 벡터 2행 1열의 값인 b와 뒤 벡터 1행 1열의 값인 c를 곱한 결과는 결과 행렬의 2행 1열에 위치한다. 앞 벡터 1행 1열의 값은 다시 뒤 벡터 1행 2열의 값과 곱하고, 결과 행렬의 1행 2열에 위치한다. 앞 벡터 2행 1열의 값은 뒤 벡터 1행 2열의 값과 곱한 후 결과 행렬의 2행 2열에 위치한다. 그럼 이때 곱한 값들의 위치는 어떻게 정해질까?

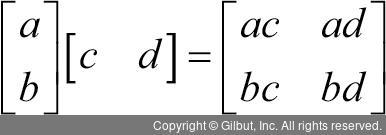
몇몇 독자는 눈치를 챘겠지만, 바로 앞 벡터에서 곱하는 값의 행 위치와 뒤 벡터에서 곱하는 값의 열 위치로 결과 행렬에서의 위치가 정해진다. 처음에는 익숙하지 않겠지만 여러 번 손으로 계산해보면 익숙해질 것이다. 이처럼 종벡터와 횡벡터의 곱은 횡벡터와 종벡터의 곱과는 완전히 다른 결과를 주며, 이를 외적(outer product)이라고 부른다.²

지금까지 우리는 행렬과 행렬의 곱에 대해 알아보았고, 그 과정에서 내적과 외적의 개념을 살펴보았다. 행렬의 곱셈은 8장에서 살펴볼 인공 신경망 계산에서 중요하게 활용된다. 이제 경우별로 내용을 정리해보자.

• 횡벡터와 종벡터의 곱: 내적을 의미하며, 스칼라가 남는다.
• 종벡터와 횡벡터의 곱: 외적을 의미하며, 행렬을 만든다.
• 행렬과 행렬의 곱: 행렬 곱셈의 방식을 따른다.
• 행렬과 벡터의 곱: 행렬과 1행(또는 1열)짜리인 행렬의 곱이며, 행렬 곱셈의 방식을 따른다.

이제 마지막으로 행렬 곱셈의 특징을 좀 더 살펴보자. 우선 일반적으로 곱셈이라 한다면 ×(곱하기) 연산자 앞과 뒤의 숫자를 바꿔도(교환해도) 결과가 동일하며 이를 교환 법칙이라고 한다. 과연 행렬의 곱셈에서도 교환 법칙은 성립할까? 실제로 행렬의 곱셈 순서를 바꾸면 결과가 다르게 나온다.

AB ≠ BA

그래서 우리는 ‘행렬의 곱셈은 교환 법칙이 성립되지 않는다.’라고 이야기한다.