지금까지 행렬의 연산에 대해 알아보았다. 이제 한 가지 더 살펴볼 내용은 바로 행렬의 의미이다. 앞에서 설명했을 때의 행렬은 벡터 여러 개를 모아 수치를 행과 열을 갖는 2차원으로 나타낸 것에 불과했었다. 하지만 행렬은 곱셈이라는 방식을 통해 계산하면 좀 더 특별한 의미를 가지게 된다. 바로 어떤 공간이나 상태를 변형시키는 것이며 이를 사영(projection)이라고 부른다.

예를 들어 한 행렬이나 벡터에 영행렬을 곱한다고 하자. 영행렬은 앞서 살펴본 바와 같이 모든 원소가 0인 행렬이다. 이 행렬을 곱하면 어떤 벡터나 행렬도 영벡터, 영행렬이 된다. 즉, 주어진 벡터나 행렬의 값이 0으로 변환하여 뿌려주게(projection) 된다. 이러한 행렬의 역할을 일종의 함수나 필터로 이해해도 좋다.

좀 더 다른 예를 살펴보자. 우리가 살펴본 행렬 중에 항등행렬이라는 것이 있었다. 대각행렬의 일종이며, 대각 위의 값이 모두 1인 행렬이었다. 항등행렬에 어떤 행렬을 곱해보자. 앞에서는 행렬의 곱셈은 교환 법칙이 성립하지 않는다고 하였는데, 이번에는 다음의 두 개의 곱셈을 살펴보자.

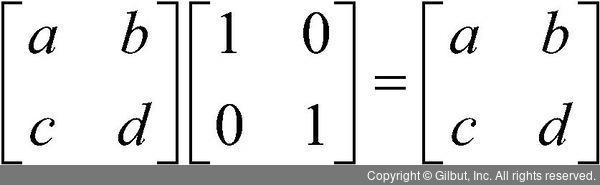
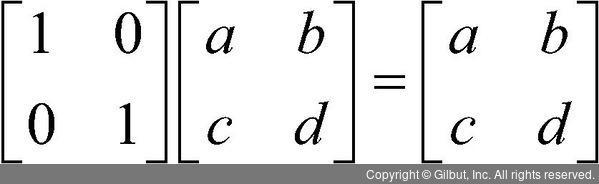
재미있게도 항등행렬에 어떤 행렬을 곱해도(행렬 곱셈이 성립된다면) 곱한 행렬이 나온다. 항등행렬을 앞에 곱하거나 뒤에 곱해도, 항상 동일한 결과가 나온다. 그래서 항등행렬은 수치의 계산에서 사용되는 항등원³과 같이 어떤 행렬을 곱해도 항상 곱한 행렬이 나온다. 즉, 항등행렬은 항상 자기 자신이 나오게 하는 함수나 필터와 같은 역할을 한다는 것을 알 수 있다.