다른 예를 살펴보자. 다음과 같은 방정식이 있다고 하자.

x' = ax + by

y' = cx + dy

여기서 x, y, x', y'는 모두 미지수이며 a, b, c, d는 모두 수치(계수)가 된다. 이 방정식은 x와 y에 a, b, c, d를 연산하여 x'과 y'를 얻는 관계를 나타낸다. x'는 x와 y에 각각 a와 b를 곱한 결과를 더해서 얻게 되며, y'는 x와 y에 각각 c와 d를 곱해서 얻을 수 있다. 이를 행렬과 벡터의 곱셈으로도 표현할 수 있다. 다음처럼 표현하고 행렬과 벡터의 곱셈을 수행하면 앞의 일차방정식과 동일하게 계산되는 것을 알 수 있다.

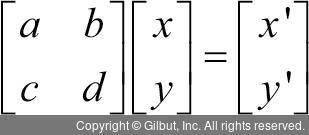
여기서 행렬은 x, y에 적절히 계산하여 x', y'를 만드는 방정식을 나타내지만 다른 관점에서 보면 x, y를 x', y'로 변환하는 필터 또는 함수와 같은 역할로 볼 수도 있다. 주어진 입력을 잘 변환하여 원하는 결과를 만들어주는 셈이다. 입력이 공간 내의 어떤 상태나 지점이었다면 행렬과 곱하여(필터를 적용하여) 변환된 공간 내의 상태나 지점을 얻을 수 있는 것이다. 이제 이러한 행렬의 곱셈이 어떻게 데이터 과학에 응용되는지를 다음 내용을 통해 살펴보도록 하자.