역행렬이 있으면 계산이 효율적이라는 것을 알 수 있는데, 그렇다면 과연 역행렬을 어떻게 구할까? 다행히도 역행렬을 구하는 공식이 이미 정리되어 있다. 다음은 역행렬을 계산하는 식이다.
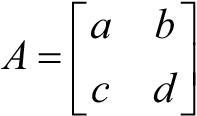
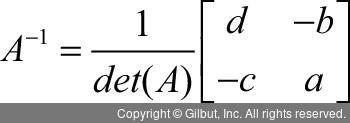
Note ≡
역행렬은 다음과 같은 특징이 있는데, 우선 A와 A의 역행렬을 곱하면 항상 항등행렬이 된다.
AA-1 = A-1A = In
또한, ABC 세 행렬의 곱셈에 대한 역행렬은 다음과 같이 나타날 수 있다. 행렬 곱셈 전체에 대한 역행렬이 있다면 곱한 행렬도 각각 역행렬이 하나씩 있다는 의미이다.
(ABC)-1 = C-1B-1A-1
그리고 A가 역행렬이 있으면 A의 역행렬도 역행렬이 있다.
A-1 = B, B-1 = A
A의 전치행렬(transpose matrix)의 역행렬은 A의 역행렬의 전치행렬과 같은 특징도 있다. 이때 전치행렬이란 기존 행렬에서 대각선을 중심으로 행과 열을 바꾸어 얻는 행렬이다. A의 전치행렬은 AT로 표현한다.
(AT)-1 = (A-1)T
이때 det(A)를 행렬 A의 행렬식(determinant)이라 하며, 그 값은 스칼라 즉, 숫자가 된다. A의 행렬식을 구하는 방식은 다음과 같다.
|A| = ad - bc