이원일차방정식으로 두 미지수 x와 y로 구성된 식이 두 개 있다. 이때 x와 y의 위치를 눈여겨보자. 미지수인 x와 y는 식에서 순서대로 나오며 두 식에 모두 등장한다. 미지수 앞에 붙은 숫자를 계수(coefficient)라고 부르는데, 계수만 따로 보면 첫 번째 행은 2와 3, 두 번째 행은 1과 -2인 행렬로 볼 수 있다. 그렇다면 방정식의 좌변은 계수로 구성된 행렬에 x와 y로 구성된 벡터를 곱한 것과 같다. 앞의 방정식을 조금 다르게 표현하면 다음과 같다.

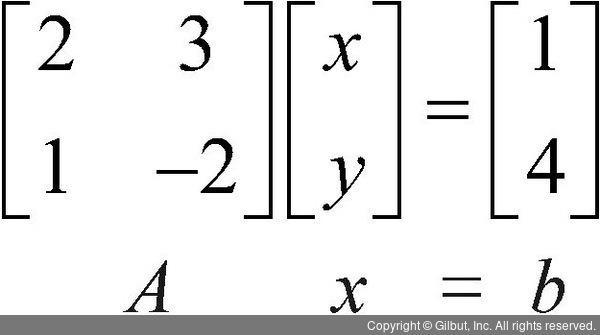
계수로 구성된 행렬을 A, 미지수로 구성된 벡터를 x라고 하면 앞의 방정식 좌변은 A와 x의 곱으로 나타난다. 그리고 방정식의 우변은 1과 4로 구성된 벡터 b가 된다.

우리가 알고 싶은 것은 바로 미지수로 구성된 x라는 벡터 값이다. 어떻게 구할 수 있을까? 앞서 살펴본 역행렬을 떠올려보자. A의 역행렬을 구할 수 있는지 확인해보고, 가능하다면 양변에 곱해보자. 같은 역행렬을 양변에 곱하면 식의 등호는 그대로 유지된다(등식의 양변에 같은 값을 곱하면 등호는 유지된다). A의 역행렬은 다음과 같이 구할 수 있다.

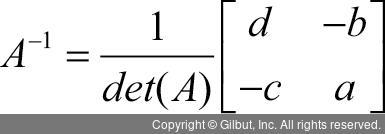
그리고 행렬식 det(A)는 다음과 같이 구한다.

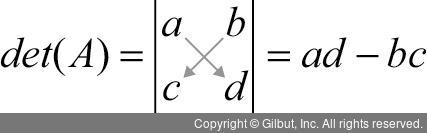
(2 × -2) - (3 × 1) = -4 + (-3) = -7