이 예에서는 0이 아닌 -7이 나온다. 이제 걱정 없이 역행렬의 식에 행렬식 값인 -7을 넣어 A의 역행렬을 구해보자.

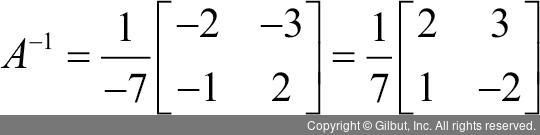
이제 이 역행렬을 원래의 방정식을 나타냈던 등식 Ax = b의 양변에 동일하게 곱하자. 곱할 때 행렬의 곱셈에서 교환 법칙은 성립되지 않음에 유의해야 한다.

A^-1Ax = A^-1b

좌변의 A^-1A는 역행렬 정의에 의해 항등행렬 I가 나온다. 그리고 항등행렬에는 어떤 값을 곱해도 곱한 값이 다시 나오니 좌변은 벡터 x만 남는다. 이제 우변을 살펴보자. A^-1b의 값은 다음처럼 A의 역행렬과 벡터 b의 곱을 통해 직접 계산할 수 있다.

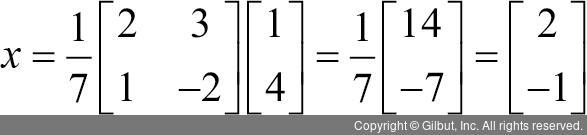
즉, 미지수 벡터는 2와 -1의 값을 갖고, 원래 알고자 한 미지수 x는 2, 미지수 y는 -1이 됨을 알 수 있다. 결과적으로는 행렬을 활용하여 일차방정식이 해결된 셈이다.

행렬의 곱셈과 역행렬을 사용해 일차방정식의 해를 구하는 것은 대표적으로 행렬을 활용한 방법이다. 다음 절에서는 이러한 행렬의 성질이 데이터 분석에서 어떻게 사용되는지 살펴보겠다.