2.5.1 분석모형 응용 - 마르코프 체인

러시아의 수학자 안드레이 안드레예비치 마르코프는 1907년에 재미있는 확률 모형을 제안하였다. 예를 들어 오늘 비가 왔는데, 내일 비가 오거나 안 오는 경우가 있다. 모든 경우는 확정적이지 않고 확률적(stochastic)으로 발생한다. 이제 내일로 넘어가보자. 내일도 모레도 비가 오거나 안 오는 경우가 있다. 과거의 경험으로 오늘 비가 왔을 때 내일 비가 올 확률은 0.6, 안 올 확률은 0.4로, 오늘 비가 안 왔을 때 내일 비가 올 확률은 0.5, 안 올 확률도 0.5로 가정했다.

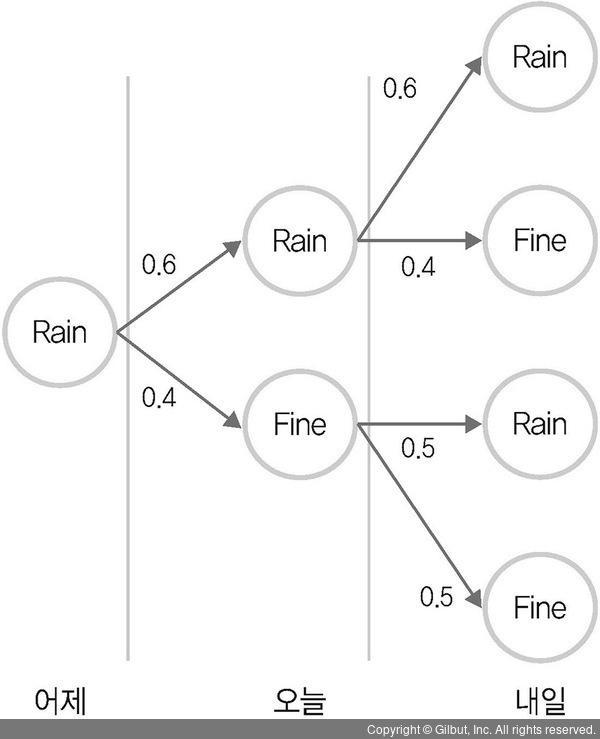
▲ 그림 2-13 어제부터 내일까지 비 오는 경우의 수

이때 우리가 관심을 갖는 비가 오거나, 안 오는 것을 ‘상태(state)’라고 부를 수 있다. 이처럼 연쇄적으로 어떤 상태를 확률 모형화한 것을 마르코프 체인(Markov Chain)이라 한다. 마르코프 체인은 현실 세계에서 상태 변환이 확률적으로 이뤄지는 시스템에 많이 적용된다.

이러한 마르코프 체인을 좀 더 쉽게 사용하려면 앞의 그림 2-13을 좀 더 간결하게 표현하는 것이 유리하다. 물론 어제, 오늘, 내일의 모든 상태 간 관계를 나타낼 수는 없지만, 매일매일 상태가 전이(transition)되는 관계를 그림 2-14처럼 표현할 수 있다.

▲ 그림 2-14 오늘 강수 여부에 따른 내일 강수 확률

즉, 오늘 비가 왔는지만 알면 내일 비가 오는지, 안 오는지를 파악할 수 있다. 예를 들어 오늘 비가 왔으면 내일 비가 올 확률은 0.6이 된다. 반면, 오늘 날씨가 좋았는데 내일 비가 올 확률은 0.5가 된다. 이 행렬은 상태 간 전이를 알려주며 행에서 출발해 열로 나가는 관계를 갖고 있고, 이를 전이행렬(transition matrix)이라 한다.

재미있는 점은 전이행렬이 나타내는 일별 상태 간 전이 관계를 바탕으로, 모레에 비 올 확률도 예측할 수 있다는 점이다. 어떻게 할 수 있을까? 오늘 비가 왔고 내일도 비 올 확률은 0.6이 된다. 이 상태에서 모레 비 올 경우는 내일이 되었을 때 다음날 비가 오는 것이므로 0.6×0.6의 확률이다. 내일 비가 안 오지만 모레 비 올 경우의 확률은 0.4×0.5가 된다. 즉, 오늘 비가 오고 모레에 비가 올 확률은 0.6×0.6 + 0.4×0.5가 된다. 이런 식으로 가능한 네 개의 조합에 대한 확률을 모두 구해 모레의 날씨를 예측할 수 있다. 이 계산을 좀 더 쉽게 하려면 전이행렬에 전이행렬을 곱하면 된다. 전이행렬은 오늘과 내일의 날씨 관계만 알려주고, 내일의 입장에서 다시 전이행렬은 내일과 모레의 날씨 관계만 알려준다. 그렇다면 전이행렬을 두 번 곱하면 오늘을 바탕으로 모레의 날씨 상태를 알 수 있다.

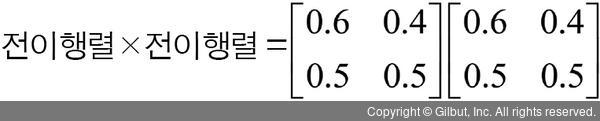
3일 후의 날씨는 전이행렬을 세 번 곱하면 되고, 4일 후는 네 번 곱하면 된다. 전이행렬을 이렇게 계속 거듭제곱하다 보면 더 이상 계산 결과가 변하지 않게 되는데, 그 관계가 장기적인 상태 간 전이 확률(steady state transition matrix)을 알려준다고 한다.

어떻게 보면 마르코프 체인은 상태 간 전이를 행렬로 구성한 후 거듭제곱하여 장기적으로 상태가 어떻게 변하는지를 예측할 수 있는 좋은 방법이 된다. 이러한 마르코프 체인을 자세히 살펴보면 더 복잡한 내용이 많이 있겠지만, 여기서는 더 깊게 들어가지 않겠다. 다만, 마르코프 체인을 통해 공학과 사회과학의 많은 현상을 효과적으로 이해할 수 있다는 점과 단순한 행렬의 곱셈만으로도 재미있는 결과를 얻을 수 있다는 점만 알아두자. 참고로 마르코프 체인은 알파고에 사용된 강화학습에서도 중요하게 활용되며, 베이지안 통계학에서도 사용되고 있다.