색칠된 부분은 항등행렬이 되어서 다음처럼 표현된다.

=PDIDIDIDIDIDIDIDIDIDP^-1

=PDDDDDDDDDDP^-1

대각에만 값이 있는 대각행렬 D를 거듭제곱한다면 대각 위 원소만 거듭제곱해도 결과 행렬을 계산할 수 있다. 그리고 나서 P와 P의 역행렬만 계산하면 복잡한 계산을 간단하게 수행할 수 있다.

행과 열이 10,000개인 행렬의 곱셈은 각 행렬에 원소 1억 개가 있고, 두 행렬의 곱셈에서는 1억 개 원소 간의 내적을 구해야 한다. 하지만 대각화를 한다면 대각 위 원소 10,000개만 제곱하여, 즉 P와 P의 역행렬만 곱하면 답을 구할 수 있다.

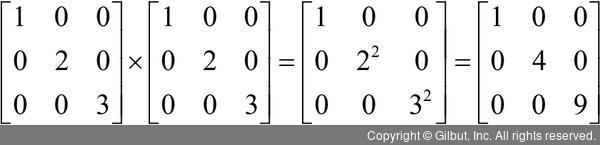
이러한 대각화는 주어진 행렬을 다른 행렬의 곱으로 나타낸 것이고 분해(decomposition)라는 표현을 사용하기도 한다.

그렇다면 행렬의 분해는 단지 계산을 쉽게 하기 위해서만 사용할까? 사실 행렬의 분해는 데이터 분석에 도움이 되기도 한다. 그중 많이 사용되는 것이 바로 행렬의 고윳값(eigenvalue, characteristic value)과 고유 벡터(eigenvector, characteristic vector)를 찾아주는 고윳값 분해다.

행렬과 벡터를 곱하면 새로운 값을 갖는 벡터가 결과로 나온다. 원래의 벡터는 행렬에 의해 변형이 일어나 새로운 벡터가 되고, 이때 행렬은 벡터를 선형 변환시킨다. 그리고 우리는 주어진 행렬 A에 대해서 다음을 만족하는 x와 λ를 고유 벡터와 고윳값으로 정의한다.

Ax = λx