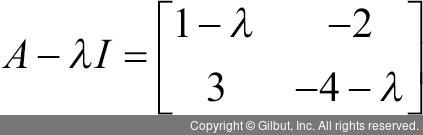이때 A는 n×n 행렬이고, x는 원소를 n개 갖는 벡터, λ는 상수가 된다. 앞의 식을 만족하는 x와 λ가 있다면 행렬 A를 x와 λ로 알 수 있다. 즉, 벡터 x를 행렬 A로 선형 변환한 Ax 값이 벡터 x와 λ를 곱한 값과 같게 된다. 앞의 식을 다시 표현하면 (A - λI)x = 0이 되며, I는 n×n 항등행렬이 되며 (A - λI)도 행렬이 된다.

(A - λI) x = 0

이 식에서 x가 0이 아닌 해를 가지기 위해서는 행렬 (A - λI)가 역행렬을 가지면 안 된다. 행렬(A - λI)의 역행렬이 존재하면 x는 0이라는 값을 갖게 되기 때문이다. (A - λI)의 역행렬이 나오지 않게 하려면 (A - λI)의 행렬식이 0이 되어야 하며, 이는 x가 0이 아닌 해를 가질 필요충분조건이 된다.

det(A - λI) = 0

우리는 이 식을 A의 특성방정식(characteristic equation)이라고도 지칭하며, 이 방정식을 풀면 고윳값인 λ를 찾을 수 있다. 그리고 고윳값을 찾은 후에는 Ax = λx에 λ를 대입하여 x를 구할 수 있으며 이 값이 고유 벡터가 된다. 즉, A를 λ와 x로 나타낼 수 있다.

이제 주어진 행렬 A의 고윳값과 고유 벡터를 구하는 간단한 예제를 살펴보자.

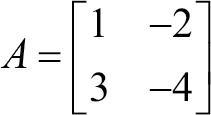
행렬 A에서 λI를 뺀 결과는 다음과 같다. 이때 I는 2×2 항등행렬임을 기억하자.