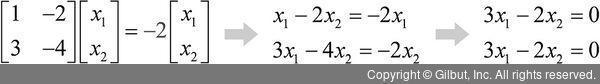그리고 행렬 A - λI의 행렬식을 구하면 다음과 같다.
det(A - λI) = (1-λ)(-4-λ) - (3)(-2) = λ2 + 3λ + 2
이때 앞서 살펴본 정의에 의해 행렬식의 값은 0이 되어야 한다. 그러므로 다음의 방정식을 푸는 문제로 바뀌게 된다.
λ2 + 3λ + 2=0
이 방정식은 중고등학교에서 배운 방식으로 해결하면 (λ + 1)(λ + 2) = 0으로 변경하여 λ는 -1 또는 -2를 갖는다. 혹은 근의 공식에 대입해서 해를 구할 수도 있다.
λ의 값이 -1이나 -2이므로 각각을 Ax = λx를 다르게 표현한 (A - λ)x = 0에 대입해보자.
우선 -1을 대입하면 고유 벡터의 두 원소는 같은 값이라는 해가 나온다.
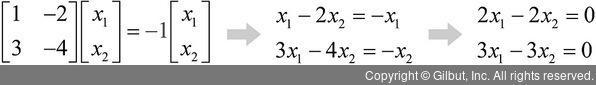
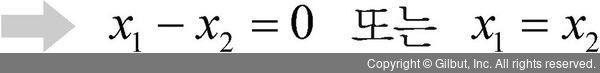
같은 값이라는 것을 t라는 매개변수로 표현하면 다음과 같다.
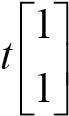
즉, 고윳값 -1에 대한 고유 벡터는 위와 같이 
에 t 배수인 벡터로 표현이 된다.
이제 고윳값이 -2인 경우를 살펴보자.
