이 식을 만족하는 고유 벡터의 값은 3x₁=2x₂ 관계를 만족하고 다음처럼 표현할 수 있다.

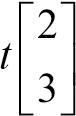
이제 고유 벡터를 다 구했다.

고윳값과 고유 벡터를 구하는 과정을 살펴보며, 한 가지 의문이 들었을 것이다. “도대체 왜 이렇게 계산을 해야할까!” 사실, 고윳값과 고유 벡터는 어떤 행렬의 특징을 알려주는 역할을 한다. 사람으로 치면 키와 몸무게처럼, 행렬도 고유한 특징의 값을 갖기 때문이다. 고윳값과 고유 벡터는 행렬의 어떤 특징을 나타내는 것일까? 이전에 행렬은 일종의 필터 역할을 한다고 했다. 필터라는 것은 한 벡터를 공간에서 다른 벡터로 변환시켜주는 것을 의미한다. 이때 공간상에서 벡터가 변환한다는 것은 벡터의 크기(magnitude)와 방향(direction)이 바뀌는 것을 의미한다. 그리고 행렬이 갖는 고유한 특징인 고유 벡터와 고윳값에 따라, 어떤 벡터는 어떤 행렬이 고유하게 갖는 크기와 방향으로 변환하기도 한다. 이때, 고윳값은 그 크기를 나타내는 역할을 하며(내적을 거치며 길이가 바뀐다), 고윳 벡터는 방향을 나타내는 역할을 하는 것이다. 그 행렬만이 갖는 변환의 특징을 잘 잡아낸 것이 고윳값과 고유 벡터인 셈이다.