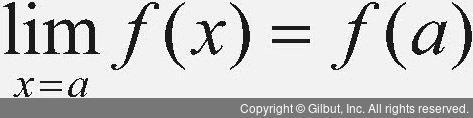3.1.2 미분과 적분을 이해하기 위한 몇 가지 개념
미분과 적분을 이해하려면 다음 몇 가지 개념을 살펴보는 것이 좋겠다. 우선, 함수의 극한과 연속성에 대해 살펴보자.
우리는 앞에서 함수라는 개념에 대해 배웠다. 디리클레의 정의에 따르면 두 변수 x와 y에 대해 x값이 정해지면 이에 따라 y값이 정해질 때 y를 x의 함수라고 하였다. 이러한 함수의 극한이란 무엇일까?
Note ≡ 함수의 극한 정의
f 함수가 x = a에서 극한값 L을 갖는다는 의미로, 아무리 작은 양수 ε이라도 상응하는 양수 δ가 존재하여 0 < |x - a| < δ일 때 |f(x) - L| < ε이 성립한다.
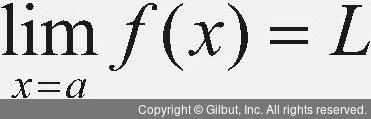
코시에 의한 정의를 먼저 살펴보면 어떤 f 함수가 x = a에서 극한값 L을 갖는다는 것은, L을 중심으로 ‘아무리 작은’ 개구간을 잡더라도 a를 중심으로 상응하는 ‘충분히 작은’ 개구간이 존재하여, 이 구간에 속하는 모든 점(a는 제외)의 함수 값이 처음 취한 ‘아무리 작은’ 구간에 속하는 것을 의미한다. 예를 들어 x→2일 때 f(x) = x2+1의 극한은 5가 되는 것이다. 간단히 말하면 함수의 입력 값이 어느 특정한 값에 아주 가까워질 때 함수가 갖는 값이 극한이다.
함수의 극한이 성립되려면 함수의 연속성이 필요하다. 함수의 연속성에 대한 개념은 함수의 그래프로부터 직관적으로 판단할 수 있다. 함수의 그래프에서 불연속점이 발견되면 연속적이지 않은 함수로 고려한다. 이러한 함수의 연속성은 19세기에 열역학에 대한 열연구부터 보다 엄밀한 수학적 의미가 요구되어 나타나게 되었다. 1821년 코시에 의해 함수의 연속성의 정의가 이루어졌으며, 극한의 개념을 필요로 한다. 다음 정의를 살펴보자.
Note ≡ 함수의 연속성 정의
f 함수가 x = a에서 연속이라는 것은 그 점에서의 극한값과 함수 값이 존재하고 두 값이 일치함을 의미한다. f가 정의역 D의 모든 점에서 연속이면 f를 연속 함수라 한다.