쉽게 설명하면 함수 그래프가 끊임 없이 매끄럽게 이어지면 그 함수는 연속이라고 정리할 수 있다. 이때 함수가 폐구간 [a, b]에서 연속이면 함수가 최댓값과 최솟값을 갖는 특징이 있고 이를 최대 최소 정리(extreme value theorem)라 한다.

다음으로는 중간값 정리(Intermediate value theorem)가 있다. 어떤 함수가 폐구간 [a, b]에서 연속이고 f(a)와 f(b)의 값이 같지 않은 조건에서 f(a)와 f(b) 사이의 어떤 값 k에 대해 f(c) = k인 c가 적어도 한 개 이상 존재하는 것을 의미한다. 다음 그림 3-5를 보면 a에서 함수 값 f(a)는 b에서의 함수 값 f(b)보다 작다. f(a)와 f(b) 사이의 어떤 y값, 여기서는 k가 되는데, 이 값을 지나는 직선은 a와 b 구간에서 f 함수와 적어도 한 번 이상 만나게 됨을 알 수 있다.

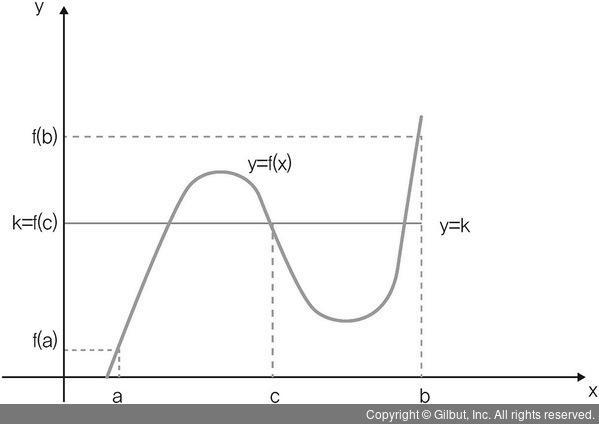
▲ 그림 3-5 중간값 정리 예시

지금까지 몇 가지 개념은 살펴봤다. 이러한 개념들은 미분과 적분의 바탕이 된다. 실수의 부분 집합 위에서 정의된 함수에 대한 극한의 개념으로 전개된 이론이 바로 미분과 적분이다. 이때 미분은 뉴턴(Newton)과 라이프니츠에 의해 발견되었고, 적분은 아르키메데스(Archimedes)에 의해 구분구적법과 유사한 실진법으로 알려지게 되었다. 이후 라이프니츠는 미적분학을 기호화하여 발전의 토대를 제공하였다.