앞서 살펴본 시간에 따른 판매량 그림을 다시 살펴보자. 일반적으로 신제품은 초기에 판매량이 더 많고 시간이 갈수록 판매량이 줄어드는 경향을 보인다. 이를 좀 더 정량적으로 표현하는 방법은 무엇일까? 우선 그림을 통해 직관적으로 이해해보자.

그림 3-7처럼 특정 시점에서 함수의 그래프가 갖는 변화하는 정도를 통해 판매량을 파악할 수 있을 것이다. 구체적으로 특정 시점에서 함수의 그래프가 나타내는 값의 변화 정도를 회색 화살표로 나타낼 수 있으며, 이는 그래프가 갖는 증감의 변화를 알려주는 매 순간의 기울기가 된다. 이러한 회색 화살표를 일반화하여 나타낸 것을 도함수라 한다.

함수의 극한이 정의되면 도함수와 정적분(definite integral)의 정의도 가능하다. 도함수는 함수의 국소적 또는 순간적인 특징을 나타내며, 정적분은 함수의 전체적인 특징을 나타낸다. 다음 도함수의 정의를 보자.

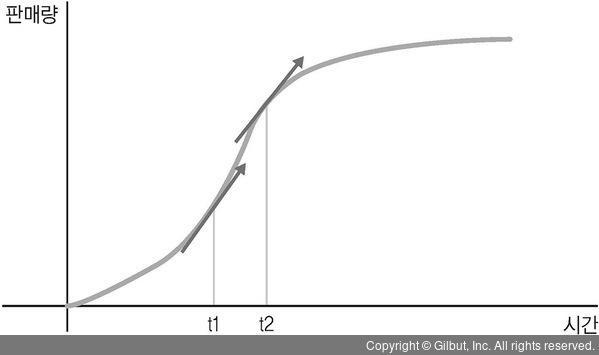
▲ 그림 3-7 시간에 따른 판매량과 변화율