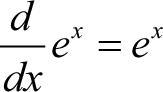위의 도함수가 x = a에서 어떤 실수로 존재하면 f가 x = a에서 미분 가능하며, 그 실숫값을 f '(a)로 표현한다. 그리고 f가 정의역 D의 모든 점에서 미분 가능하면 f는 미분 가능 함수(differentiable function)라 부른다.

이때 도함수 f '도 함수이므로 미분이 가능하며, 도함수, 도함수의 도함수, 도함수의 도함수의 도함수를 각각 1계, 2계, 3계, … 도함수라 부른다. 1계도함수는 변화량의 함수, 2계도함수는 변화량의 변화량 함수, 3계도함수는 변화량의 변화량의 변화량 함수이며 다음처럼 표시할 수 있다.

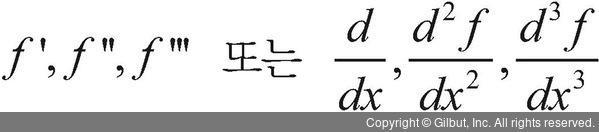
앞에서 살펴본 바와 같이 어떤 관계의 변화량을 알 수 있다는 것은 우리가 현상을 이해하는 데 많은 도움이 된다. 그러한 ‘변화량’을 이해하는 방법인 도함수를 실제로 구하려면 다음의 몇 가지 수식을 먼저 살펴보자. 가급적 딱딱한 수식을 지양하면 좋겠으나, 도함수의 이해를 위해서 도함수에 대한 다양한 형태를 살펴보겠다. 만약 f, g 함수가 미분 가능하고, a, b가 상수라면 다음 등식들이 성립한다. 이 등식들은 각 미분 계산에 많이 사용되니 참고하자.

• X의 n차항을 미분하는 방법

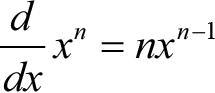
• Logx를 미분하는 방법

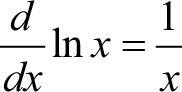
• 지수를 미분하는 방법