3.3.1 리만 적분 또는 정적분

앞의 과정을 수학적으로 나타내 보자. 한 폐구간 [a, b]를 작게 나누는데, 분할된 간격들이 갖는 최댓값의 극한이 0에 가까워질 때 (즉, 면적을 구하기 위한 사용한 직사각형의 너비가 아주 좁게 될때) 분할된 x의 간격에 상관없이 다음의 극한값이 존재하면 함수 f는 적분 가능(integrable)하다.

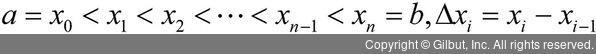
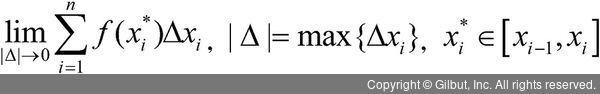
이렇게 구하게 되는 극한값을 f의 정적분 또는 리만(Riemann) 적분이라고 부르며 수식은 다음과 같다.

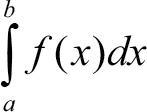
만약 함수 f(x)가 폐구간에서 연속이면 적분 가능하고, 또는 단조증가하면 그때도 적분이 가능하다. 이러한 적분은 다음과 같이 파이썬을 통해서 실행할 수 있다. 앞에서 봤던 f(x) = 3x²+1을 적분하는 경우를 생각해보자. 이번에도 미분에서 사용했던 심파이의 integrate 함수를 사용해 적분해보자.

>>> import sympy as sp
>>> x = sp.Symbol('x')
>>> sp.integrate(3.0*x**2+1, x)
1.0*x**3 + 1.0*x

또는 사이파이 라이브러리를 사용할 수 있다. 다음 코드는 적분한 다음 x가 0~2일 때까지의 적분한 값을 계산한 것이다. 결과를 보면 소숫점 밑에 숫자가 붙는데, 이는 사이파이에서 사용하는 알고리즘 때문에 발생하는 것이다.

>>> import numpy as np
>>> from scipy.integrate import quad

>>> def f(x):
>>>     return 3.0*x**2 +1
>>> i = quad(f, 0, 2)
>>> print(i[0])
10.000000000000002