3.4.1 미적분학의 기본정리
우선 미적분학의 기본정리를 이해하려면 먼저 평균값 정리를 살펴봐야 한다. 평균값 정리는 미분 가능한 함수의 그래프에서 시작한다. 평균값 정리에 따르면 그래프 위, 임의의 점 두 개의 기울기와 그 두 점 사이의 어떤 점의 기울기가 같은 것이 적어도 한 개는 존재한다. 평균값 정리는 곡선의 기하학적 특성을 도함수로 표현할 수 있으며, 미적분학의 기본정리를 전개할 때 사용된다.
Note ≡ 평균값 정리 정의
함수 f가 폐구간 [a, b]에서 연속이고 개구간 (a, b)에서 미분 가능하면 개구간 (a, b) 안의 적어도 하나의 점 x1이 존재하여 다음이 성립된다.
f(b) = f(a) = f '(x1)(b - a)
그리고 연쇄 법칙을 볼 수 있는데, 연쇄 법칙은 함수 f와 g가 미분 가능한 함수일 때 합성 함수 h = f·g는 미분 가능한 함수이고, 그 도함수는 h'(x) = f '(g(x))g'(x)로 나타낼 수 있음을 의미한다.
이제 이 개념을 바탕으로 미적분학의 기본정리(fundamental theorem of calculus)에 대해 살펴보자. 이 정리는 리만 적분을 계산하기 위해 피적분함수 f(x)의 역도함수(antiderivative)인 F(x)를 구하는 것과 관련이 있다.
만약 함수 f가 폐구간 [a, b]에서 연속이고 개구간 (a, b)에서 미분 가능하며 f의 역도함수가 F이면 F의 도함수가 함수 f가 되어 다음과 같이 나타낼 수 있다.
F '(x) = f(x)
또한, 함수 F와 함수 f의 관계를 바탕으로 다음과 같이 나타낼 수 있다.
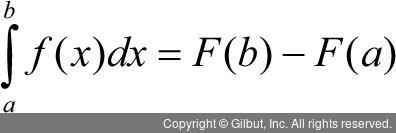
그리고 도함수 f '(x)를 나타내는 또 다른 기호로 dy/dx를 사용하며 y = f(x)를 미분하며 dy = df(x) = f '(x)dx로 정의된다. 미적분학의 기본정리가 미분과 적분으로 연결된다 정도로 이해하자.