즉, 2차식 함수를 미분해 얻은 1차식이 0일 때의 x값을 찾는 것이, 최적의 값(최소값)을 찾는 문제의 해가 된다. 이때 사이파이를 사용하면 함수의 해를 찾는 것은 쉽게 구할 수 있다. 다음 코드는 y = x + 3 함수가 0이 될 때의 x값을 찾는 문제다.

>>> from scipy.optimize import fsolve
>>> import numpy as np
>>> line = lambda x: x + 3
>>> solution = fsolve(line, -2)   # 해를 -2부터 찾기 시작한다
>>> print(solution)
[-3.]

지금까지는 미분을 이용해 함수의 해를 찾는 것을 알아보았다. 이 문제를 더 확장하여, 다변수 함수의 미분과 적분을 살펴보자. x에 해당하는 변수가 여러 개인 다변수 함수에서 사용되는 도함수를 우리는 편도함수(partial derivative)라 부른다. 예를 들어 함수 z = f(x, y)는 x, y 두 변수를 가지며, 이 함수를 미분한 것이 바로 편도함수이다. 미분하는 방법은 y를 상수로 고정하는 경우, z는 x로만 구성된 1변수 함수로 볼 수 있는데, 만약 그 함수가 미분 가능하면 x에 대한 도함수를 얻을 수 있다. 이렇게 얻어진 도함수를 f의 x에 관한 편도함수라고 하며 ∂f/∂x로 표현한다. 그리고 x에 관한 편도함수는 partial derivative of f with respect to x로 읽을 수 있다.

이렇게 다변수 함수에서 여러 개의 편도함수를 구할 수 있고, 다변수 함수의 모든 편도함수를 다음처럼 한 묶음으로 표현할 수 있는데 이를 그라디언트 벡터(gradient vector)(기울기 벡터)라 부른다. 함수 f(x, y, z)의 그라디언트 벡터는 다음과 같다.

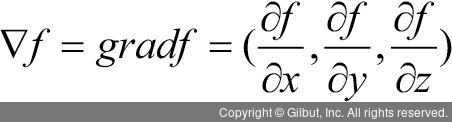
이때 여기서 ∇은 편미분 연사자(∂/∂x, ∂/∂y, ∂/∂z)를 표시하는데, 그라디언트 벡터는 매끄러운 곡면 f(x, y, z) = 0에 수직인 법선 벡터이다. 즉, 곡면 위의 임의의 점을 잡았을 때 그 점을 지나는 곡면 위의 모든 곡선의 접선 벡터에 수직인 벡터를 나타내게 된다.