역시 1을 얻었다. 그리고 처음 얻은 해가 정확히 1이 아닌 이유는 뉴턴랩슨 메서드가 수치적으로 해에 접근하는 방식때문이다.
# f의 미분된 함수를 또 미분한 함수를 표시 >>> root = optimize.newton(f, 1.5, fprime2 = lambda x: 6 * x) >>> print(root) 1.0000000000000016 >>> root = optimize.newton(f, 1.5, fprime = lambda x: 3 * x**2, fprime2 = lambda x: 6 * x) >>> print(root) 1.0
경사 하강법은 함수 위의 임의의 점에서 시작하여 함수에서 계산한 기울기의 반대 방향으로 움직여가며 국소 또는 전역 최솟값에 도달하는 방법이다. 이해를 위해 다음의 간단한 예제를 살펴보자.
우리는 x = 3에서 시작하여 y = (x + 5)2의 국소 최솟값(local minima)을 찾고자 한다. 가장 직관적인 방법은 그래프를 통해 최솟값을 찾는 것이다.
다음 그림 3-13을 보자. y = (x + 5)2 함수의 그래프에서 x가 -5일 때 최솟값인 0을 갖게 된다. 그러므로 이 함수의 국소 및 전역 최솟값은 -5가 된다.
하지만 컴퓨터가 수식이나 그래프를 보고 최소 지점을 직관적으로 이해하고 답 -5를 바로 내놓기란 쉽지 않다. 그러면 똑같은 결과를 기계적이고 수치적으로 발견하기 위해 경사 하강법을 사용해 보자.
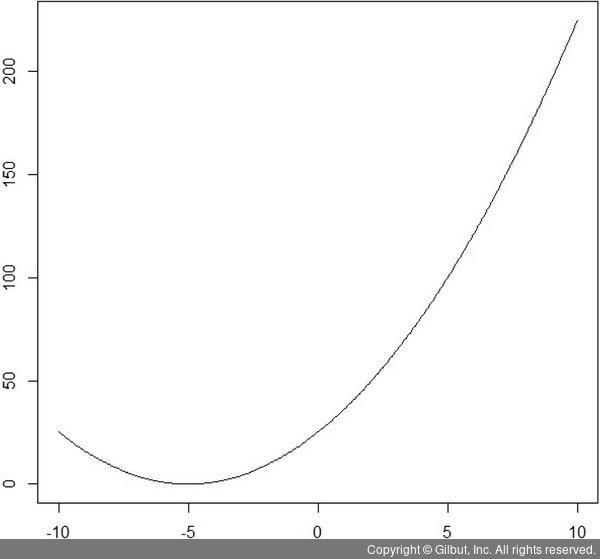
▲ 그림 3-13 y=(x+5)2 그래프