우선 단변수 통계량 중에서 집중화 경향에 속하는 통계량을 살펴보자. 대표적인 것으로는 산술 평균(mean)이 있다. 평균은 mean, arithmetic mean, average 등의 용어로 나타내며, 여러 값의 중심 또는 균형점을 나타낸다. 평균으로 자료의 중심을 효율적으로 나타낼 수 있다. 한 변수에 속하는 모든 관측값의 크기(정보)를 반영해야 하며 평균을 구하는 방법은 모든 값을 더해서 값의 개수로 나누는 것이다. 평균은 간단하면서 쉽게 여러 값들의 중심을 나타낼 수 있어서 많이 사용되는 대표적인 통계량이다.

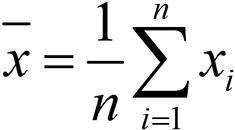
반면에 이상값(outlier)의 영향을 받는다는 단점이 있다. 예를 들어 네 명의 머리 둘레의 평균을 구하는데, 첫 번째 집단에는 100, 105, 95, 100의 값이 있고, 평균은 100이 된다. 두 번째 집단에는 150, 100, 100, 100의 값이 있고, 평균은 112.5가 된다. 두 집단 대부분은 머리 둘레가 비슷하지만, 두 번째 집단에는 머리가 아주 큰 사람이 있다 보니 관측값과 평균은 차이가 많이 난다. 즉, 이러한 이상값의 영향을 받아 평균이 실제 값과 다르게 계산될 수 있는 단점이 있다.

다음으로 중앙값(median)이 있는데, 이는 관측값을 크기순으로 나열하였을 때 중앙에 위치하는 관측값을 의미한다. 평균과는 다르게 이상값에 덜 민감하다. 다만, 값의 개수가 홀수인 경우는 문제가 없지만, 짝수인 경우에는 중앙에 속하는 두 관측값의 평균으로 구한다.

▲ 그림 4-3 중앙값의 예