이제 가장 많이 사용되는 산포도인 분산과 표준편차에 대해 살펴보자. 분산(variance)은 각 관측값이 평균에서 얼마나 퍼져있는지를 보는 척도이다. 각 관측값과 평균의 차이가 있고, 그 차이들의 평균을 나타낸 것이다. 모집단으로부터 분산을 구하면 이는 모분산(population variance)이 된다.

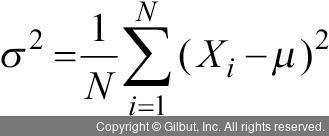
표본에서 얻은 분산은 표본 분산(sample variance)이라고 하며, 다음처럼 구한다.

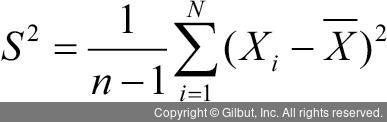
다음 그림 4-5와 같이 분산을 구하려면 먼저 관측값과 평균의 차이를 제곱해야 한다. 이 값들은 각 관측값이 평균과 떨어진 정도를 의미하는데, 관측값의 개수만큼 계산된다. 이 값들을 효율적으로 요약하려면 이 값들의 평균을 구해야 하는데, 이게 바로 분산이다.

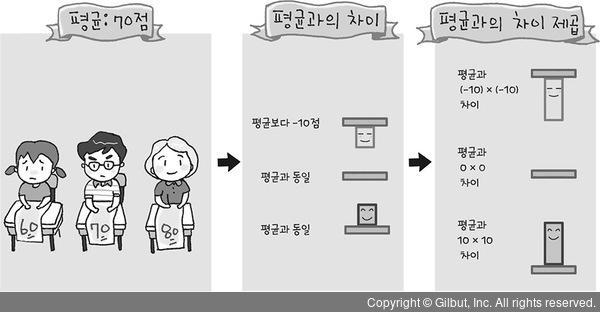
▲ 그림 4-5 분산의 계산 과정

분산을 구하는 과정에서 관측값과 평균의 차이를 제곱하는 이유는 관측값과 평균의 차이에서 음수가 나올 수 있는데 이때 제곱하지 않고 더하게 되면 값들끼리 상쇄되어 원래 퍼진 정도와 다른 값이 나오기 때문이다. 이렇게 제곱하여 계산했기 때문에 모분산이나 표본 분산의 측정 단위는 관측값과 평균의 차이를 측정한 크기보다 커진다. 사실 우리가 알고 싶은 것은 각 관측값이 평균과 대체로 어느 정도 차이 나는지이지만, 분산은 평균과의 차이를 제곱한 값으로 원래 알고자 한 크기가 제곱되어 나타난다. 그렇기 때문에 분산을 원래 알고자 하던 크기로 바꾸려면 분산값의 양의 제곱근을 사용해야 한다. 이를 표준편차(standard deviation)라 한다.