상관관계 역시 두 변수의 증감 관계를 보기 위한 통계량인데, 두 변수의 공분산을 바로 각 변수의 표준편차로 나눠 구한다. 이렇게 하면 값은 언제나 -1~1 사이의 값으로 조정된다. 표준편차라는 것은 그 변수가 갖는 변수의 중심으로부터의 평균적인 퍼짐 정도라고 볼 수 있으며, 일종의 값의 단위가 된다. 이러한 표준편차로 공분산을 각각 나누면 변수의 크기로 인한 부분이 제거가 되어 두 변수의 증감에 대한 관계만 남는다. 그래서 두 변수의 공분산이 각 변수의 절대적 크기에 영향을 받지 않도록 각 변수의 표준편차로 나눠준 버전(scaled version)을 상관관계라 한다. 대표적인 상관관계로는 피어슨의 상관관계(Pearson correlation)가 있으며, 다음과 같이 구할 수 있다.

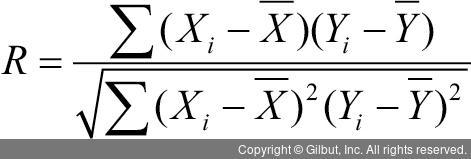
앞서 살펴본 바와 같이 상관관계는 -1~1 사이의 값으로 주어지는데, 1은 두 변수 간 강한 양의 상관관계가 있음을, 0은 관계가 없음을, -1은 강한 음의 상관관계가 있음을 의미한다. 즉, 두 변수의 증감 관계를 좀 더 표준화된 통계량으로 볼 수 있다. 예를 들어 어떤 상관관계가 0.9이고, 다른 상관관계가 0.7이면 우리는 변수 크기의 단위에 상관없이 0.9인 상관관계가 더 강하다고 얘기할 수 있다.