두 사상에 대해서 각 발생할 확률과 동시에 발생할 확률을 구해서 비교해보자. 앞에서 P(A∩B) = P(A)P(B)가 성립한다면 두 사상은 독립, 그렇지 않다면 조건부 확률을 고려할 수 있다.

여기서 주의할 점은 두 사건의 독립은 P(A∩B) = P(A)P(B)를 의미하지만, P(A∩B) = 0을 나타내지는 않는다는 것이다.

다시 조건부 확률로 돌아오자. 조건부 확률은 두 사건 A, B에 대해 P(A) > 0일 때 사건 A가 참인 조건 하에서 사건 B가 일어날 확률을 의미하는데, 앞서 살펴본 표본 공간의 관점에서 본다면 원래의 표본 공간은 S이지만, 조건부 확률에서는 조건이 되는 사건 A가 표본 공간의 역할을 하는 셈이다. 조건부 확률 역시 확률이므로 0~1 사이의 값을 가지며, 조건이 되는 사상의 자기 자신에 대한 조건부 확률은 P(A|A) = 1로 나타난다.

이제 조건부 확률 식을 잠깐 변경해보자.

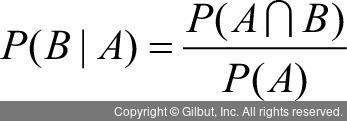
이때 곱의 법칙(multiplication rule)을 이용하여 앞의 식에 0이 아닌 값을 양변에 곱해도 등호가 유지된다.

P(A∩B) = P(A)P(B|A) = P(B)P(A|B)

위의 관계를 바탕으로 우리는 다음과 같은 식을 생각할 수 있다.

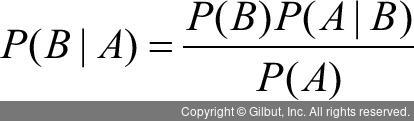
이를 베이즈 정리(bayes theorem)라고 부르며, 확률 변수의 조건부(conditional) 확률 분포와 주변부(marginal) 확률 분포를 연관 짓는 정리이다. 확률 분포에 대한 내용은 5장에서 자세히 다루니, 여기서는 베이즈 정리를 새로운 자료에서 나온 확률에 기반하여 과거의 확률을 향상(update)하는 관계로 이해해보자. 앞의 식에서는 B의 확률이 원래 있었는데, 새롭게 얻은 자료인 A와 B의 관계를 나타내는 확률을 이용하여 결과적으로 A가 주어진 경우 B의 조건부 확률로 향상하게 된다.