다음의 예를 살펴보자. 한 마트에서 손님 7명이 구매한 내역이 다음 표 4-2와 같다. 손님 7명 중에서 소고기를 산 손님은 4명으로, 산술적으로 오늘 마트에서 소고기가 팔릴 확률은 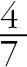가 된다. 손님들은 여러 물건을 구매하였으니, 이제 여러 제품의 조합에 대해 팔릴 확률을 구할 수 있다. 여러 제품의 조합을 이제부터 판매되는 제품의 패턴으로 고려하자.

소고기와 닭고기를 모두 구매한 손님은 7명 중에서 3명이고, 발생 확률은 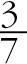이 된다. 이제 소고기를 사는 조건에서 닭고기를 사는 경우도 생각해보자. P(닭고기|소고기)를 구하는 문제가 되며, 전체 손님 중 소고기를 사는 확률 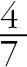가 분모가 되고, 닭고기와 소고기를 같이 사는 확률 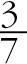이 분자가 되어 계산할 수 있다. 이 조건부 확률은 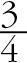의 값을 가지며 이 값이 바로 신뢰도가 된다.

▼ 표 4-2 손님들의 구매 목록

이제 옷을 사는 경우, 우유와 닭고기를 사는 패턴에 대해서 지지도를 구하면 전체 손님 7명 중에서 옷, 우유, 닭고기를 같이 산 손님이 3명이므로 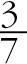이 된다. 그 경우 신뢰도를 구하면 옷을 산 손님이 우유와 닭고기를 사는 조건부 확률이므로 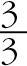의 값을 가진다. 이렇게 손님의 구매 내역으로 모든 품목을 최대한 조합하여 지지도와 신뢰도를 계산할 수 있다. 분석자는 계산된 값에서 높은 지지도와 신뢰도를 갖는 것만 필터링하여 보면 된다.