5장에서는 우선 확률에 대한 개념을 확률 변수와 확률 분포로 확장하여 살펴볼 것이고, 통계량을 이용한 통계적 추론에 대해서도 살펴보겠다.

앞서 이해한 바와 같이 확률이란 특정한 사상이 발생할 정도를 0~1 사이로 계량화한 값이다. 하지만 현실에서 다루는 현상에는 여러 사상¹이 발생할 수 있으며, 그로 인해 다루게 되는 확률도 많아진다.

예를 들어 한 반의 어린이들을 대상으로 오늘 결석하였는지를 살펴본다고 하자. 어린이마다 결석이라는 사상이 발생할 확률을 측정할 수 있다. 하지만 이 반에는 어린이가 여러 명 있으며, 결석 확률 값 역시 어린이의 수만큼 존재한다. 그리고 어린이들이 모두 비슷한 결석 확률을 갖고 있을 수도 있고 아니면 특정 어린이만 높은 결석 확률을 갖고 있을 수도 있다. 이 반에서 결석이라는 사상을 잘 이해하려면 각 어린이가 발생시키는 확률 값의 분포를 이해하는 것이 중요하다.

좀 더 구체적으로 어린이들의 출석과 결석 여부를 측정한다고 하자. 여러 개의 출석 또는 결석 값이 수집될 것이고, 이 사상들에 대한 확률 값이 필요하다. 한 반에 어린이가 5~6명이면 큰 문제는 안 되겠지만, 그 수가 늘어난다면 여간 복잡한 작업이 아닐 수 없다. 이때 입력이 출석이면 숫자 1을 출력하고 결석이면 숫자 0을 출력하는 함수를 이용해서 이 작업을 정리해보자.

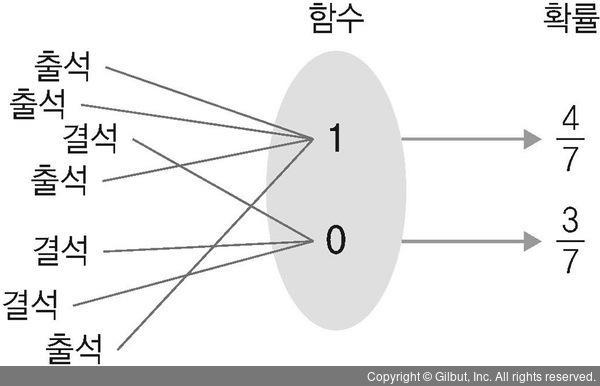
▲ 그림 5-1 출석과 결석의 확률 분포