측정치에서 얻을 수 있는 값의 총 집합을 표본 공간이라 하는데, 앞의 경우와 같이 표본 공간의 각 값에 실수를 부여하는 함수를 확률 변수라고 한다. 확률 변수는 여러 확률 값을 사상과 연결할 수 있으며, 그 결과는 확률 분포로 나타난다. 즉, 확률 분포(probability distribution distribution)는 확률 변수가 취할 수 있는 모든 값에 대해 이들 값이 취할 수 있는 확률을 그림이나 표, 함수식으로 나타낸 것이다.

표본 공간이 이산형과 연속형이 있는 것처럼, 확률 분포 역시 이산형과 연속형으로 구분할 수 있다. 이산형 확률 분포는 불량 수나 결점 수와 같이 셀 수 있는 확률 변수의 각 값에 대응되는 확률 분포를, 연속형 확률 분포는 제품이 중량이나 치수와 같이 셀 수 없는 연속 값을 갖는 확률 분포를 의미한다.

다음과 같이 동전을 던지는 상황을 가정해보자. 동전을 한 번 던지는 경우에는 표본 공간 S = {H, T} 즉, 앞면과 뒷면만 있으며, H와 T가 각 표본점이 된다. 이때 확률 변수는 각 표본점에 숫자를 대응시키는 역할을 하는 일종의 함수이다. 표본점을 입력 받고, 그 표본점에 대응하는 숫자를 출력한다.

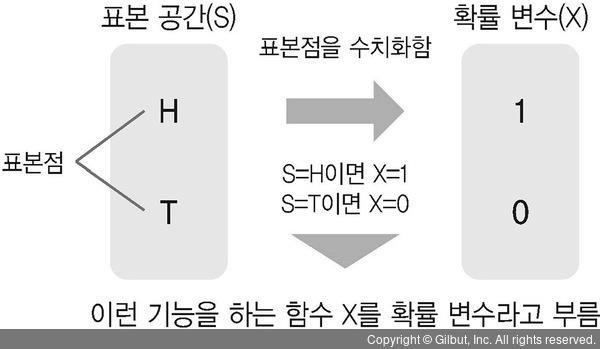
▲ 그림 5-2 동전 던지기에 대한 확률 변수

이처럼 확률 변수는 표본점 각각에 대응하여 숫자로 변환시킨다. 그렇다면 표본점을 의미하는 숫자가 발생할 확률은 각각 있을 것이며, 이러한 과정을 통해 어떤 사상의 발생에 대해 더 잘 이해할 수 있다.