특히, 확률 분포는 확률 변수의 각 출력값과 각 값에 대응하는 확률을 보여주는 모든 표, 그래프, 식 등을 의미한다. 예를 들어 다음 그림 5-3에 나오는 식도 당연히 확률 분포로 볼 수 있다.

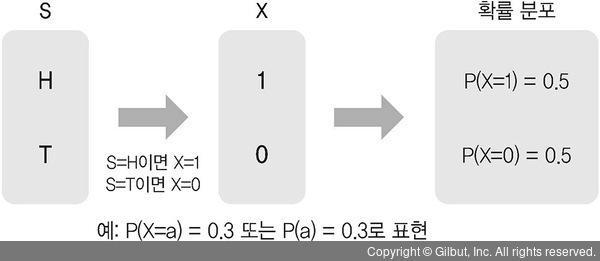
▲ 그림 5-3 동전 던지기에 대한 확률 분포

이때 알파벳 대문자는 확률 변수의 이름을 나타내고, 알파벳 소문자는 확률 변수의 값을 나타낸다. 앞의 예에서 확률 변수 X가 1일 때 확률 0.5를 표현하는 식은 P(X = 1) = 0.5로 나타낸다.

확률 변수에 대응되는 확률의 관계를 함수로 나타낸 것을 확률 분포 함수(probability distribution function)라 부른다. 확률 분포 함수는 항상 +값을 가지며, 표본 공간 안에 있는 전체 사상의 확률을 합치면 1이 된다. 즉, 어떤 사상이 각 발생할 경우에 대한 확률 값을 알려준다.

앞의 예처럼 동전을 던지는 경우에 앞면과 뒷면만 가능하다고 할 때 각 표본점의 확률은 50%가 된다. 그리고 동전을 던져 나오는 모든 경우의 확률을 더하면 100%가 된다. 그렇다면 동전 던지기처럼 모든 경우의 표본점을 명확하게 구분할 수 있을까? 연속형인 경우에는 그렇지 않을 수도 있다. 우리가 사용하는 형광등의 수명을 생각해보자. 형광등이 지금 나갈 확률 값은 확률 밀도 함수를 통해 구할 수 있다. 그렇지만 문제는 형광등이 나간 ‘지금’이라는 시점을 정확하게 잡아낼 수 있는가이다. 형광등의 수명은 시간 값이고, 시간은 계속해서 흘러간다. ‘찰나의 순간’이라는 말도 있듯이, 어느 한 시점을 잡아낼 수가 없다. 사람이 사용하는 시, 분, 초라는 개념 역시 계속 흘러가는 시간의 어떤 시점을 정확히 잡아내기에는 역부족이다.