5.2.2 포아송 분포

이번에는 대표적인 이산형 확률 분포인 포아송 분포를 살펴보자. 단위 시간이나 단위 공간에서 특정 사건이 드물게 발생할 때 그 사건의 발생 건수가 따르는 확률 분포를 포아송 분포라 부른다. 예를 들어 어느 지역의 하루 교통사고 수를 본다면 특정한 지역에서 특정한 단위 시간에 발생하는 사건의 빈도수가 되며, 이는 포아송 분포(Poisson distribution)를 따른다.

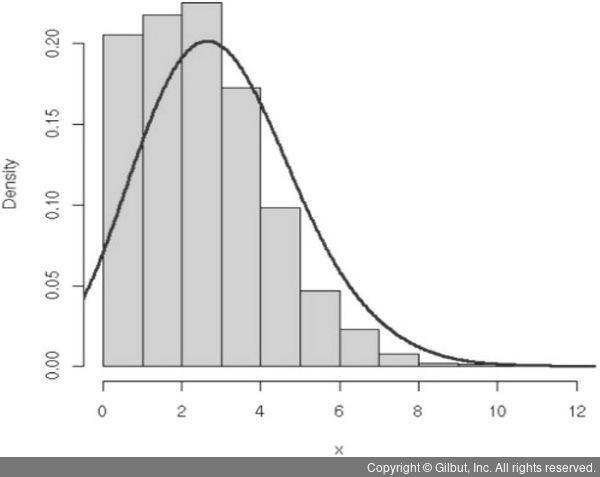
▲ 그림 5-5 포아송 분포의 예

그림 5-5에서 볼 수 있듯이, 이러한 사건의 빈도는 사건이 적게 나타나는 쪽인 왼쪽으로 치우쳐 있다. 운행 중인 자동차에서 절반이 넘게 교통사고가 발생하지 않고, 생산되는 모든 제품에서 결함이 발생하지는 않는다. 오히려 포아송 분포의 대상이 되는 사건은 주로 적은 빈도로 발생한다. 이와 비슷한 분포로 이항 분포가 있다. 어떤 사건이 발생하거나 발생하지 않는 경우를 모델링하는 이항 분포에서 해당 사건의 발생 확률인 p가 0.1 이하인 경우에는 포아송 분포로 변화한다.

이러한 포아송 분포를 나타내는 확률 밀도 함수를 다음과 같이 나타낼 수 있다.

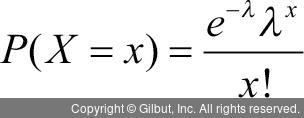
이때 λ는 사건의 평균적인 발생 빈도를 의미하고, x는 사건의 발생 횟수가 된다. 특히, 정해진 시간 안에 어떤 사건이 일어날 빈도를 나타내는 포아송 분포에서는 사건의 빈도에 대한 기댓값인 λ가 중요한 역할을 한다. λ를 안다면 해당 사건이 특정한 횟수로 발생할 때의 확률도 계산할 수 있다. 그러다 보니 λ는 포아송 분포의 평균으로 사용된다. 포아송 분포의 특징은 평균과 분산이 같다는 것이다. λ가 5보다 크다면 포아송 분포는 정규 분포로 고려할 수 있다.