어떤 구간에 속한 모든 점에서 연속적으로 값을 취할 수 있는 경우에는 연속형 확률 분포(continuous probability distribution)를 사용한다. 즉, 확률 변수 X가 취할 수 있는 값이 무한하여, 확률 변수의 확률 분포가 연속적인 곡선으로 나타난다. X가 취할 값을 특정하기 어려우므로 연속형 확률 밀도 함수는 하나의 값이 아닌 어떤 구간에서의 확률 값을 구하게 되며, 이때 적분을 사용한다. 즉, P(a≤X≤b)는 확률 밀도 함수에서 실수 a, b 구간에서의 곡선 아래의 면적이며, 이 값이 확률 값으로 사용된다. 이산형과 다른 점은 이산형 확률 변수는 특정한 값을 가질 수 있는 반면 연속형 확률 변수는 매우 작은 크기의 수치들이 연속적으로 이어져 있는 상황에서 특정한 값을 갖기가 어렵다는 점이다. 따라서 어떤 구간에서 적분을 통해 확률 값을 갖게 되는 셈이다.

예를 들어 전구의 수명 시간을 확률 분포로 나타낸다고 하자. 만약 10시간 전에 설치한 전구가 방금 고장 났다면 우리는 일반적으로 전구의 수명은 10시간이라고, 구체적인 수치로 얘기하게 된다. 하지만 방금 고장 난 그 시점, 그 찰나를 설치 후 딱 10시간으로 특정 짓기는 어렵다. 시간은 연속적으로 계속해서 흐르는 값이며, 사람의 편의상 시분초로 나누지만 사실 그보다 더 작은, 사람이 특정 지을 수 없는 무한히 작은 단위로 시간이 흘러가기 때문이다.

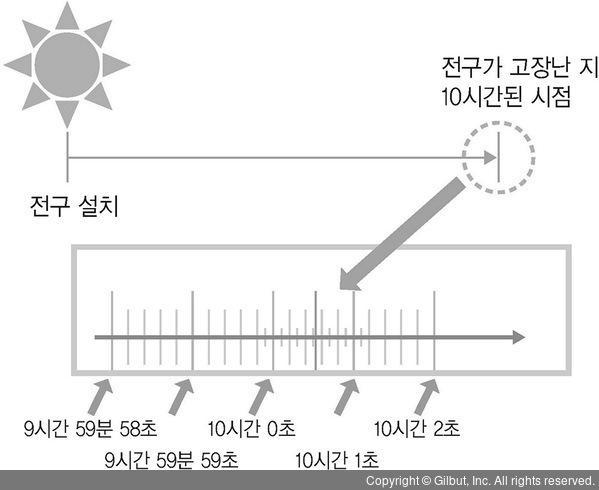
▲ 그림 5-6 전구 수명 시간의 예