그림 5-6에서 전구가 고장 난 시점은 정확히 10시간은 아니며, 10시간 근처의 어떤 한 시점이다. 우리는 10시간과 10시간 1초 사이도 아주 작은 단위로 나눌 수가 있지만, 그 어느 지점이며 이를 숫자로 특정하기란 어렵다. 연속형 확률 분포는 이러한 연속적인 값을 다루는 확률 분포이다.

이처럼 연속형 확률 변수 Y가 있을 때 확률 분포의 특징은 다음처럼 살펴볼 수 있다. 우선, 확률 밀도 함수가 나타내는 모든 확률 값을 더하면 표본 공간의 모든 대상 사건에 대한 확률 값의 합이므로(대상의 모든 발생 가능한 경우는 전체이므로) 이 값은 1이 된다. 즉, 확률 밀도 함수의 모든 구간에서의 적분 값은 1이 된다. 또한, 확률이므로 모든 구간에서 확률 밀도 함수의 값은 0보다 크다. 주의할 점은 확률 변수 Y가 a 지점일 때의 확률은 0이라는 것이다. 연속형인 경우, a 지점을 특정하기 어렵고 a라는 값은 연속형에서는 ‘찰나’로 연속적으로 흘러가는 시간의 한 순간을 의미하기 때문에(아주 작은 값), 그때의 확률은 0인 것으로 고려한다. 그래서 연속형인 경우에는 특정 구간의 확률 값을 구하는 것이다.

특정 구간에서의 확률 값도 적분으로 구할 수 있으며, 이러한 작업을 위해 누적 분포 함수(Cumulative Distribution Function, CDF)를 사용한다. 누적 분포 함수는 특정 구간에서의 확률 밀도 함수(Probability Density Function, PDF)의 값을 적분한 것으로, 대문자 F로 주로 표현한다. 확률 변수 Y가 y값까지 갖는 확률의 값은 누적 분포 함수 F를 통해 다음처럼 구할 수 있다.

누적 분포 함수: F(y) = P(Y ≤ y)

그리고 누적 분포 함수는 확률 밀도 함수의 적분이므로 다음과 같은 식도 성립한다.

확률 밀도 함수: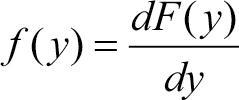

앞 장에서 살펴본 적분의 개념을 조금 더 적용해보자. 확률 변수 Y가 a값과 b값 사이에 있을 확률, 예를 들어 형광등의 수명이 a 시간보다 크고 b 시간보다 작을 확률을 구한다고 하면 우리는 확률 변수 Y가 a와 b 사이에 있을 확률을 구하는 것이다. 다음 식을 눈으로 가볍게 살펴보자.

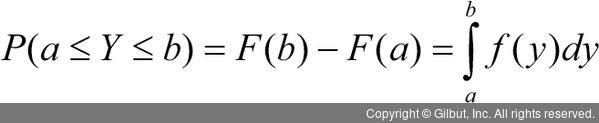
지금부터 연속형 확률 분포와 관련된 내용과 통계적 추론에 많이 사용되는 확률 분포를 살펴보겠다. 처음 접하는 경우에는 익숙하지 않을 수 있으니, 분포 이름만 기억하고 넘어가도록 하자. 너무 세부적인 내용보다는 각 확률 분포의 대략적인 특징을 이해하는 것이 효과적이다. 또한, 수식의 경우에도 처음에는 ‘이런 식이 있었구나’ 하는 정도로 확인하고 넘어가본다(물론 나중에 더 학습할 경우에는 수식도 이해를 해야 하지만…).