5.3.1 정규 분포와 중심 극한 정리

정규 분포

대표적인 연속형 확률 분표인 정규 분포(normal distribution)에는 몇 가지 특징이 있는데 우선, 정규 분포의 모양과 위치는 분포의 평균(μ)과 표준편차(σ)로 결정된다. 정규 분포의 확률 밀도 함수는 평균을 중심으로 대칭인 종 모양을 가지며, 정규 분포를 나타내는 정규 곡선(normal curve)은 X축에 맞닿지 않으므로 확률 변수 X가 취할 수 있는 값의 범위는 -∞ < X < +∞이다(관측값의 99.7%가 ±3σ 안에 속해 있다). 정규 분포의 평균과 표준편차가 어떤 값을 갖더라도 정규 곡선과 X축 사이의 전체 면적은 1이다. 정규 분포의 확률 밀도 함수는 다음과 같이 나타낼 수 있다.

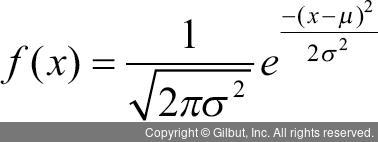
이러한 확률 밀도 함수를 바탕으로 정규 분포를 그래프로 나타낸 정규 곡선은 다음 그림 5-7과 같다.

▲ 그림 5-7 정규 분포의 예

이때 평균은 μ이고, 표준편차가 σ인 정규 분포를 따르는 확률 변수 X를 다음과 같이 표현하기도 한다.

이러한 정규 분포를 평균 μ = 0, 표준편차 σ = 1이 되도록 표준화한 것을 표준 정규 분포라고 부르는데, 어떤 관측값의 확률 분포 X를 원래 크기가 아닌 평균을 중심으로 값의 크기를 조정하고, 그 값이 평균으로부터 표준편차의 몇 배 정도나 떨어져 있는지를 나타낸 확률 분포이다. 이때 표준 정규 분포는 확률 변수 Z로 나타내며, N(0, 1²)으로 표시한다.