중심 극한 정리

평균이 μ이고 분산이 σ²인 모집단에서 표본 크기가 n이 되도록 표본을 랜덤하게 뽑는 경우를 생각해보자. 이때 표본의 크기 n이 충분히 크다면 모집단의 분포 모양에 관계없이 표본들의 평균값의 분포인 X는 근사적으로 정규 분포 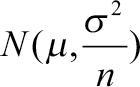를 따르게 된다. 확률 변수는 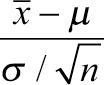로 표현할 수 있으며, 근사적으로 평균은 0이고 표준편차는 1인 정규 분포 N(0, 1)을 따른다. 모집단이 정규 분포를 따르는 경우이든, 정규 분포가 아닌 임의의 분포를 따르는 경우이든 표본의 크기가 충분히 크다면 표본 평균의 분포는 정규 분포를 따른다. 표본 평균의 분산은 표본의 크기(n)로 나눈 것만큼 작아지기 때문이다. 이를 중심 극한 정리(central limit theorem)라고 한다.