이러한 통계적 추론의 가장 중요한 부분은 바로 표본으로 모집단의 값인 모수를 추정하는 것이다. 모집단의 특성(평균, 편차 등)을 이해하려면 통계적 추론 과정을 통해 표본의 특성을 이해해야 하고, 그 특성들이 통계적으로 얼마나 신뢰할 수 있는지를 봐야 한다. 표본으로 미지의 모수를 알아내는 과정을 추정(estimation)이라고 하는데, 여기에는 점 추정과 구간 추정이 있다.

점 추정(point estimation)은 모수가 특정한 값일 것이라고 추정하는 것이다. 모수를 잘 추정하려면 좋은 통계량이 있어야 한다. 좋은 통계량의 조건으로 불편성/효율성/일치성/충족성 등을 갖춰야 한다.

• 불편성(unbiasedness): 모든 가능한 표본에서 얻은 추정량의 기댓값이다.
• 효율성(efficiency): 추정량의 분산이 작을수록 좋다.
• 일치성(consistency): 표본의 크기가 커지면 추정량이 모수에 근사한다.
• 충족성(sufficiency): 추정량이 모수에 대해 모든 정보를 제공한다.

예를 들어 표본 평균과 표본 분산을 살펴보면 모평균과 모분산을 추정하는 특정한 값이 된다. 표본 평균(sample mean)은 확률 표본의 평균값이며 다음과 같이 나타낼 수 있다.

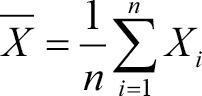
또한, 모분산을 추정하기 위한 표본 분산(sample variance)은 다음처럼 나타낼 수 있다.

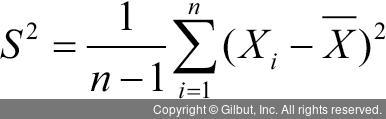
하지만 점 추정의 경우에는 모집단의 어떤 값을 정확하게 추정하는 것이므로 어떤 값의 구간을 추정하는 것보다 어려울 수 있다. 그래서 사용하는 것이 바로 구간 추정(interval estimation)이다. 즉, 점 추정의 정확성을 보완하기 위해 확률로 표현된 믿음의 정도 하에서 모수가 특정한 구간에 있을 것이라고 선언하는 것이다. 구간 추정을 하려면 추정하려는 통계량의 확률 분포에 대한 전제가 필요하고, 추정하려는 구간 안의 모수가 있을 가능성의 크기(신뢰 수준)가 필요하다. 즉 어떤 통계량이 95% 신뢰 수준 하에서 모평균의 신뢰 구간에 있는 것을 보는 것이 구간 추정이다. 이를 위해서 추정량의 분포에 대한 전제를 바탕으로 모수가 있을 것으로 예측되는 신뢰 구간(confidence interval)을 구한다.