검정 통계량으로 사용되는 상관계수(correlation coefficient, r)는 두 집단 간의 직선적인 관계를 나타내는 지표로 -1~1 사이의 값을 가진다. 두 변수의 공분산을 각 변수의 표준편차로 나눠준, 일종의 표준화된 공분산의 개념이다. 앞서 살펴본 공분산이 두 변수의 변하는 정도를 선형적으로 파악한 것이라면 상관계수는 이러한 공분산을 -1~1 사이의 크기로 변환한 것이다. 다음은 상관계수를 구하는 식이다.

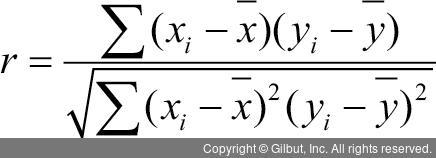
그림 6-1은 상관계수가 나타내는 대표적인 선형 관계를 보여준다. 상관계수가 1에 가까울수록 ‘양의 상관’으로, x값이 늘어나면 y값도 늘어나는 관계이다. 반면 -1에 가까울수록 ‘음의 상관’으로, x값이 늘어나면 y값은 줄어드는 관계이다. 여기서 상관계수가 0이 되면 선형 관계가 뚜렷하게 없음을 의미한다.

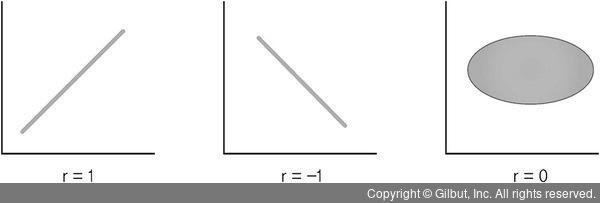
▲ 그림 6-1 상관계수가 나타내는 선형 관계

상관분석으로 두 변수에 대해서 선형 관계를 파악할 수 있다. 이러한 상관분석을 하기 전에 우선, 산점도를 이용해 두 변수의 개략적인 선형 관계를 파악하는 것이 중요하고, 또한 상관계수를 계산할 때 영향을 줄 수 있는 이상값의 존재 여부를 확인하는 것도 필요하다. 만약 산점도를 그렸을 때 두 변수가 직선적인 관계가 아니라면 상관분석을 해도 결과가 의미있지는 않을 것이고, 직선적인 관계에서 벗어나는 이상값이 있는 경우에는 오히려 상관관계를 왜곡할 수도 있다. 즉, 산점도를 그려서 선형 관계가 보이지 않거나 이상값이 많은 (튀는 값이 많은) 경우에는 상관분석이 적절하지 않다.