6.2.1 일원 분산분석
일원 분산분석부터 살펴보자. 우선, 분산분석을 하려면 평균과 집단을 나타내는 변수가 필요하다. 이때 우리가 보려는 것은 평균의 차이이기 때문에 평균을 구하는 변수가 우리의 목적이 되는 변수로, 종속 변수가 된다. 반면에 집단을 나타내는 변수는 범주형 변수이며, 독립 변수가 된다.1
이처럼 종속 변수에는 수치형 값을 갖는 연속형 자료(continuous data)가, 독립 변수에는 수치형이 아닌 범주형 자료(categorical data)가 있는 경우, 분산분석을 사용할 수 있다. 앞서 얘기한 것과 같이 우리의 목적은 평균의 차이를 보는 것이기 때문에 이때 종속 변수는 평균을 구할 수 있는 수치형 값을 가져야 한다. 반면, 독립 변수는 바로 집단을 표현하는 범주 값을 가져야 하며, 이를 범주형 자료라고 한다. 그리고 독립 변수에는 범주형 변수의 각 범주를 나타내는 요인의 수준을 고려하여 사용한다. 종속 변수의 평균을 독립 변수의 요인별로 구해서 비교하는 것을 일원 분산분석이라 한다.
다음의 예를 살펴보자.
▼ 표 6-1 분산분석에 사용되는 자료의 형태
|
요인 |
관측값 |
평균 |
|
요인의 수준 1 |
Y11, Y12, … Y1n |
|
|
… |
… |
… |
|
요인의 수준 R |
Yr1, Yr2, … Yrn |
|
표 6-1에서 전체 Y값의 평균은 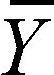 이고, 또한 요인의 수준별로 자료를 나누어서 각 평균을 구할 수 있다. 각 요인에 속한 개별 관측값은
이고, 또한 요인의 수준별로 자료를 나누어서 각 평균을 구할 수 있다. 각 요인에 속한 개별 관측값은  로 나타나는데, 이때 사용된 첨자를 살펴보면 다음과 같다.
로 나타나는데, 이때 사용된 첨자를 살펴보면 다음과 같다.
- i = 1, 2, …, r은 요인(factor)의 수준(level)
- j = 1, 2, …, n은 각 요인의 수준에 해당하는 관측값의 개수
- μi: i번째 수준에서의 평균
- Yij, εij: 각 i번째 수준에서 측정된 j번째 값과 이때의 오차를 의미한다. 오차라는 것은 해당 요인의 수준에 속한 개별 값과 해당 요인 수준의 평균의 차이이다. 특히 오차 εij는 서로 독립이며, 정규 분포 N(μi, σ2)를 따른다고 가정한다.
1 2장에서 종속 변수, 독립 변수에 대해서 배웠다.
 (수준 1 관측값의 평균
(수준 1 관측값의 평균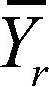 (수준
(수준