위와 같이 관측된 자료를 요인의 수준별로 나누어 정리했다면 분산분석의 절반 이상은 해결한 셈이다. 우리가 알고 싶은 것은 독립 변수가 갖는 요인의 수준에 따라 종속 변수의 평균 차이가 있는지인데, 그러기 위해서는 ‘자료 전체에서 얻은 값’을 ‘요인의 수준별로 자료를 분류해 얻은 값’과 비교를 하는 것이 자연스럽다. 분산분석은 종속 변수 관측값의 전체 변동을 비교하려는 요인 수준 간 차이에 의해서 발생하는 변동과 그외 요인에 의한 변동으로 나누어 분석하는 기법이다. 즉, 개별 관측값과 전체 관측값 평균의 차이는 다음과 같이 나눌 수 있다.

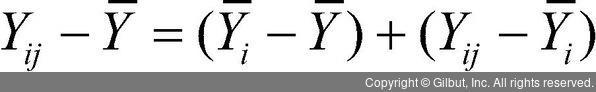
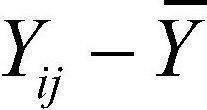• : 개별 관측값 － 전체 관측값의 평균
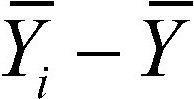• : 요인 수준 i에서 관측값의 평균 － 전체 관측값의 평균(수준 i에 의한 변동)
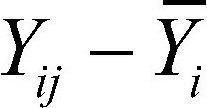• : 개별 관측값 － 요인 수준 i에서 관측값의 평균(수준 i에 의해 설명될 수 없는 변동)

이처럼 어떤 개별 값과 전체 값의 평균의 차이는 그 개별 값이 속한 요인의 평균을 고려하여 두 개의 값(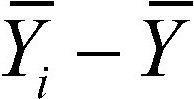, 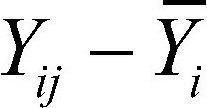)으로 나눌 수 있다. 문제는 우리가 다루는 자료는 한 개의 값만 있지 않다는 것이다. 이런 계산을 통해 나온 여러 개의 값이 존재하니, 이제 이 값들을 하나의 값으로 표현해보자. 이때 사용하는 것이 제곱합이다. 굳이 제곱해서 더해주는 이유는 어떤 관측값은 평균보다 작을 수도, 클 수도 있는데 단순하게 더하면 값들끼리 상쇄되는 경우가 발생하기 때문이다. 각 값들이 평균과 ‘얼마나’ 차이가 있는지가 중요한 정보인데, 더하면 이 정보들이 사라질 수 있으니 제곱해서 더하는 방법을 사용하는 것이다.

이제 위의 식 양변을 제곱하여 더하면 SST = SSTR + SSE로 표현할 수 있으며 식으로는 다음과 같이 나타낼 수 있다.

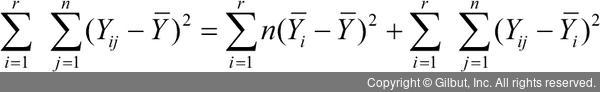
SST = SSTR + SSE

• SST: 전체제곱합(Total Sum of Squares)
• SSTR: 처리제곱합(Treatment Sum of Squares)
• SSE: 오차제곱합(Error Sum of Squares)