6.2.3 이원 분산분석
일원 분산분석과 다르게 이원 분산분석(two-way ANOVA)은 한 관측값을 두 요인의 수준별로 조합하여 평균 차이를 비교하는 분석이다. 예를 들어 요인 ‘크기’에서 요인 수준이 세 개(대, 중, 소)가 있고, 요인 ‘맛’에는 요인 수준이 두 개(맛있음, 맛없음)가 있으면 총 그룹의 수는 3 × 2 = 6개가 된다. 6개의 요인 조합에 속하는 값들의 평균을 비교한다. 이때 관측값이 한 개일 경우와 두 개 이상일 경우(똑같은 그룹에 대해 또다시 종속 변수를 측정하는 반복 실험을 할 경우)로 구분할 수 있는데, 여기서는 관측값이 하나인 경우만 살펴보겠다.
다음 표 6-4를 보면 두 요인의 수준이 각 행과 열에 나타나지며, 이때 각 값은 관측값이다.
▼ 표 6-4 이원 분산분석을 위한 두 요인의 수준별 관측값
|
|
수준 1 |
… |
수준 b |
평균 |
|
수준 1 |
Y11 |
… |
Y1b |
|
|
… |
… |
… |
… |
|
|
수준 a |
Ya1 |
… |
Yab |
|
|
평균 |
|
|
|
|
이때 이원 분산분석의 편차  는 다음과 같이 구분할 수 있다.
는 다음과 같이 구분할 수 있다.

 =개별 관측값 - 전체 관측값의 평균
=개별 관측값 - 전체 관측값의 평균 = 요인 A의 수준 i 관측값의 평균 - 전체 관측값의 평균
= 요인 A의 수준 i 관측값의 평균 - 전체 관측값의 평균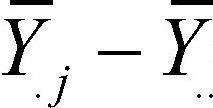 = 요인 B의 수준 j 관측값의 평균 - 전체 관측값의 평균
= 요인 B의 수준 j 관측값의 평균 - 전체 관측값의 평균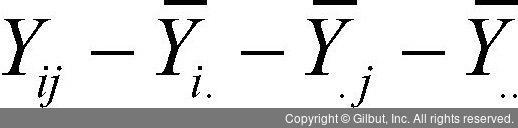 = 개별 관측값 - 요인 A의 수준 i 관측값의 평균 - 요인 B의 수준 j 관측값의 평균 - 전체 관측값의 평균
= 개별 관측값 - 요인 A의 수준 i 관측값의 평균 - 요인 B의 수준 j 관측값의 평균 - 전체 관측값의 평균

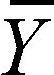 a
a