일원 분산분석과 마찬가지로, 앞의 식을 제곱합한 후 다음 식처럼 나타낼 수 있다.
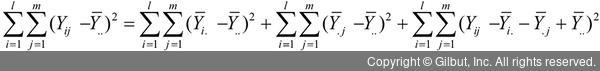
SST = SSA + SSB + SSE
- SST: 전체제곱합(자유도 = ab - 1)
- SSA: 요인 A 수준 평균 간 제곱합(자유도 = a - 1)
- SSB: 요인 B 수준 평균 간 제곱합(자유도 = b - 1)
- SSE: 오차제곱합(자유도 = (a - 1)(b - 1))
이러한 이원 분산분석의 값들을 일목요연하게 정리하여 제시한 것을 이원 분산분석표(two-way ANOVA Table)라 한다. 다음 표 6-5를 살펴보자.
▼ 표 6-5 이원 분산분석표
|
|
제곱합 |
자유도 |
평균 제곱 |
F 통계량 |
|
요인 A |
SSA |
a - 1 |
MSA |
MSA/MSE |
|
요인 B |
SSB |
b - 1 |
MSB |
MSB/MSE |
|
오차 |
SSE |
(a - 1)(b - 1) |
MSE |
|
|
계 |
SST |
ab - 1 |
|
|
이원 분산분석의 편차(
)는 다음과 같이 구분할 수 있으며 이를 F 통계량으로 검정한다.
- 요인 A의 수준에 따른 평균 차이가 있는지를 검정(검정 통계량: MSA/MSE(F 통계량) )
- 귀무 가설(H0): A의 수준에 따라 평균 차이가 없다.
- 대립 가설(H1): A의 수준에 따라 평균 차이가 있다.
- 요인 B의 수준에 따른 평균 차이가 존재하는지를 검정(검정 통계량: MSB/MSE(F 통계량))
- 귀무 가설(H0): B의 수준에 따라 평균 차이가 없다.
- 대립 가설(H1): B의 수준에 따라 평균 차이가 있다.