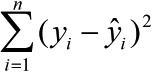그렇다면 직선을 어떻게 그려야 두 변수를 잘 나타낼 수 있을까? 이 질문에 답하는 과정이 바로 앞의 두 미지수를 구하는 과정이다. 이에 앞서 잔차라는 개념을 먼저 살펴보자. 잔차(residual)는 선형 회귀 식에 의해 각 예측한 Y와 실제 Y의 차이를 나타낸다. 다음은 잔차의 식이다.

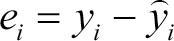
즉, 잔차라는 값은 실제 Y값이 직선으로 표현되는 Y값(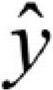로 표현함)에서 얼마나 떨어져 있는지를 알려준다. 그림 7-5에서 보면 각 점들은 실제 Y값이고, 주황색 직선은 예측된 Y값을 나타낸다. 각각의 실제 Y와 예측한 Y의 차이는 회색 실선으로 나타내고 이 회색 실선이 잔차이다.

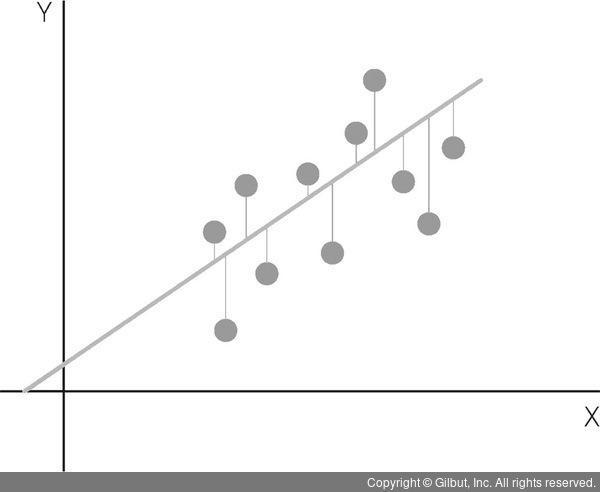
▲ 그림 7-5 잔차의 표현

잔차는 바로 예측값과 실제 값의 차이이기 때문에 가급적 작을수록 좋다. 개별 Y값이 아닌 전체 Y 값들의 관점에서도 잔차들을 모두 더한 것이 작아야 좋겠지만, 여기에 한 가지 문제가 있다. 바로 실제 값이 예측값보다 작은 경우에는 잔차가 음수로 나와서 양수인 잔차와 더해지면 즉, 실제로 각 잔차가 있음에도 불구하고 모든 잔차를 더하면 그 값이 0이 되는 문제가 발생한다. 그렇기 때문에 잔차의 제곱을 모두 더해서 잔차제곱합이 최소가 되게 하는 직선을 찾아야 한다. 그러한 직선의 미지수 Y 절편과 기울기를 찾는 것이 선형 회귀 분석이다.