통계적 추론을 위해 선형 회귀 분석에서는 잔차의 확률 분포에 대해 몇 가지를 가정한다. 잔차의 등분산성과 정규성을 갖는다는 가정이다. 이는 잔차가 모두 같은 분산을 갖는 정규 분포를 따른다는 것을 의미한다. 물론, 기본적으로는 종속 변수와 독립 변수의 선형성에 대한 가정과 확인이 전제되어야 한다.

이렇게 잔차의 제곱합을 최소화하는 Y 절편과 기울기를 찾는 방법을 최소제곱법(Least Squares Estimation)이라 한다. 앞의 식에서 예측한 Y는 다시 두 미지수가 포함된 X에 대한 식으로 치환할 수 있으며, 그 값이 최소가 되는 두 미지수를 찾기 위해서는 이 식을 각 미지수로 적분을 한 값이 0이 되면 된다. 그렇게 되면 미지수가 두 개이고, 식도 두 개인 방정식을 푸는 문제가 되어 다음과 같은 식을 통해 구할 수 있다.

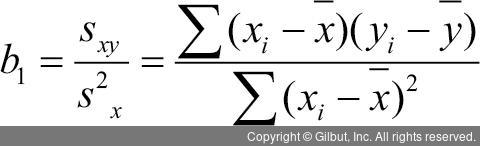
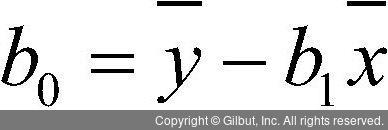
선형 회귀 분석을 하는 과정에서 우리는 앞의 식을 직접 계산하지는 않는다. 그저 선형 회귀 분석의 결과로 나온 기울기와 절편만 해석하면 된다. 그렇지만 앞에서 설명한 과정을 이해하는 것은 해석하는 데 많은 도움을 준다.