지금까지는 하나의 종속 변수와 하나의 독립 변수인 경우를 바탕으로 직선을 구하는 방법을 살펴보았다. 하지만 실제로 분석할 때는 독립 변수가 여러 개 주어진다. 이때에도 선형 회귀 분석을 할 수 있으며, 이것을 다중 선형 회귀 분석이라 한다. 선형 회귀 분석은 독립 변수가 종속 변수에 어떤 효과를 주는지를 모형화하는 데 사용하고 특히, 어떤 변수가 변화할 때 다른 변수들도 그 변화량에 각 기울기를 곱한 만큼 변화하는 것을 가정한다. 여러 개의 독립 변수에 대해서도 이러한 해석은 마찬가지이며, 다음과 같은 식처럼 모형을 통해 각 Y를 예측한다.

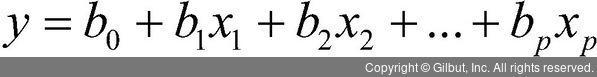
다중 선형 회귀 분석의 해석은 기본적으로 독립 변수가 한 개인 선형 회귀 분석과 동일하지만 독립 변수 간의 다중공선성(multicollinearity)이 있는지를 주의해야 한다. 즉, 독립 변수와 종속 변수의 관계가 주요 관심사인데, 독립 변수끼리 직선적 관계가 크다면 원래 목적인 독립 변수와 종속 변수 관계를 왜곡시킬 수 있다.

이처럼 데이터에 적합한 선형 회귀모형인 직선을 찾았다면 과연 이 모형이 데이터를 얼마나 잘 설명하고 있는지에 대한 검정이 필요하다. 이러한 모형에 대한 검정은 크게, 모형 자체에 대한 검정과 변수 X가 갖는 계수에 대한 검정으로 나누어 볼 수 있다.

우선 각 독립 변수 앞에 붙는 기울기를 살펴보자. 이 기울기는 회귀계수라고 부르게 되는데, 회귀계수의 의미는 해당 변수 X가 변수 Y와 갖는 직선적 관계이다. 즉, 분석하기 전에는 변수 X와 Y의 관계는 밝혀지지 않았음을 의미하고 이를 회귀계수=0으로 표현한다. 그 회귀계수에 해당하는 독립 변수는 종속 변수와 관계가 없다고 해석할 수 있다.