분석 후 계산된 회귀계수에 대해서는 변수 X와 Y의 관계가 있음을 의미한다. 지금까지의 지식은 회귀계수=0이었는데, 분석을 통해서 얻은 새로운 지식은 회귀계수≠0가 된다. 앞서 살펴본 통계적 가설 검정의 틀을 그대로 사용해보자. 기존 지식인 회귀계수=0을 귀무 가설로 고려하고, 우리가 계산한 회귀계수≠0는 대립 가설로 고려한다. 그리고 다음의 통계량을 통해 각 독립 변수의 회귀계수(기울기)에 대한 가설을 검정한다.

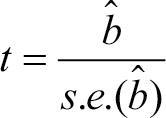
앞의 통계량이 검정에 사용되니 검정 통계량이라 부르자. 검정 통계량으로 우리는 유의 확률인 p값을 구해서 가설 검정을 할 수 있다. 유의 확률이 주어진 유의 수준(일반적으로 5%)보다 작은 경우 귀무 가설을 기각하고, 분석을 통해 계산된 0이 아닌 회귀계수가 유의하다고 해석한다. 이때 회귀계수의 크기는 독립 변수가 종속 변수에 미치는 영향의 크기를 나타낸다.

선형 회귀 분석에 대한 검정의 또 다른 방향은 바로 모형 자체에 대한 검정이다. 이때 우리는 결정계수(R²)를 사용하며, 결정계수 계산에 사용되는 개념을 다음처럼 정리하였다.

• 전체제곱합(SST): 실제 종속 변수와 예측한 독립 변수의 차이를 제곱하여 더함, 회귀제곱합과 잔차제곱합으로 나눌 수 있다.
• 회귀제곱합(SSR): 예측한 각 종속 변수에서 예측한 종속 변수의 평균을 뺀 값을 제곱
• 잔차제곱합(SSE): 실제 각 종속 변수에서 예측한 종속 변수의 평균을 뺀 값을 제곱

선형 회귀모형은 X와 Y의 복잡한 관계를 어느 정도 직선식의 모양으로 단순화시킨다. 그러다 보니 선형 회귀모형을 수립하면 실제 Y와 모형으로 예측한 Y의 차이가 Y개만큼 발생하는데, 여기서 발생하는 차이 값들을 요약한 것이 SST가 된다. 그리고 이 값은 독립 변수인 X에 의해 발생하는 부분과 그외의 부분으로 구분할 수 있다.

예측한 각 Y에서 예측한 Y의 평균을 뺀 부분을 회귀제곱합이라 하여 독립 변수에 의해 설명되는 부분으로 고려한다. 즉, 별다른 모형 없이도 우리는 Y의 평균을 기대할 수 있는데, 예측한 Y와 예측한 Y의 평균 차이가 변수 X에 의해 설명되는 것으로 본 셈이다.