그리고 예측한 Y의 평균에서 실제 각 Y를 뺀 값의 제곱합을 모형에 의해 설명되지만, 독립 변수로는 설명되지 않는 부분을 잔차제곱합이라 한다.
그렇다면 모형을 수립했을 때 좋은 모형이라 부르는 경우는 모형을 통해 선택한 변수 X가 변수 Y를 잘 설명하는 것이다. 앞서 살펴본 SST, SSR, SSE 값을 이용하여 모형이 데이터를 얼마나 잘 설명하는지를 구할 수 있는데, 이 값이 결정계수가 된다. 결정계수는 회귀제곱합/전체제곱합으로 구한 값으로, 이 값이 1에 가까울수록 회귀모형이 데이터를 잘 설명한다고 이해할 수 있다.
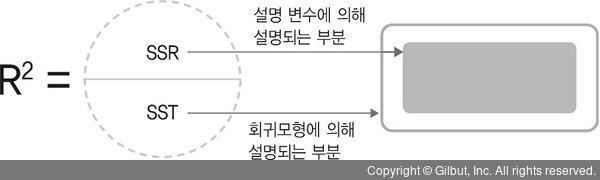
▲ 그림 7-6 결정계수
이제 다음의 실습을 통해 회귀 분석을 이해해보자. 우선, 변수 x와 y를 가지는 데이터를 만들고 두 변수의 직선식 관계를 찾아보고자 한다. 이 예에서 x는 일주일 동안 공부한 시간을, y는 성적을 나타낸다. 학생 10명의 공부 시간과 성적에 대한 데이터는 다음과 같다.
>>> import numpy as np >>> data = np.array([[100,30 ], >>> [80, 20], >>> [90, 26], >>> [50, 15], >>> [70, 20], >>> [80, 22], >>> [75, 23], >>> [60, 15], >>> [100, 35], >>> [20, 2]]) >>> x = data[:,1].reshape(-1, 1) # x의 열이 한 개일 경우, 열 개수 정보를 추가 >>> y = data[:,0] >>> print(data) array([[100, 30], [ 80, 20], [ 90, 26], [ 50, 15], [ 70, 20], [ 80, 22], [ 75, 23], [ 60, 15], [100, 35], [ 20, 2]])