선형 회귀모형은 변수 Y가 수치인 경우에 사용된다. 엄밀하게 Y는 수치이면서 잔차의 분포는 등분산을 갖고, 잔차는 정규 분포를 따르는 것으로 가정한다. 심지어는 변수 X와 Y의 관계가 선형 관계여야 한다. 만약 변수 Y가 수치형 데이터이지만, 앞서 얘기된 조건을 만족하지 못하는 경우는 어떻게 될까? 선형 회귀 분석의 사용 조건을 만족하지 못하는 Y는 생각보다 많다. 예를 들어 0보다 큰 빈도를 갖는 Y를 생각해보자. 이때 Y를 빈도(count data)라 하는데, 이때 일반적인 선형 회귀모형을 사용하면 올바른 결과를 도출하기 어려울 것이다. 이 빈도에 대해서는 다른 종류의 회귀모형을 사용하는데 그게 바로 포아송 회귀모형(poisson regression)이다. 포아송 회귀모형은 X와 Y의 관계가 비선형인 경우, 특히 Y값이 이산적이며 0이나 1에 많이 쏠린(skewed) 경우에 사용된다. 이때 Y는 이분산(heteroskedasitc)하여 등분산성이라는 가정을 만족시키지 못한다. 일반적인 선형 회귀 분석에서는 Y의 예측값이 양수만 나오도록 하기는 어렵다.

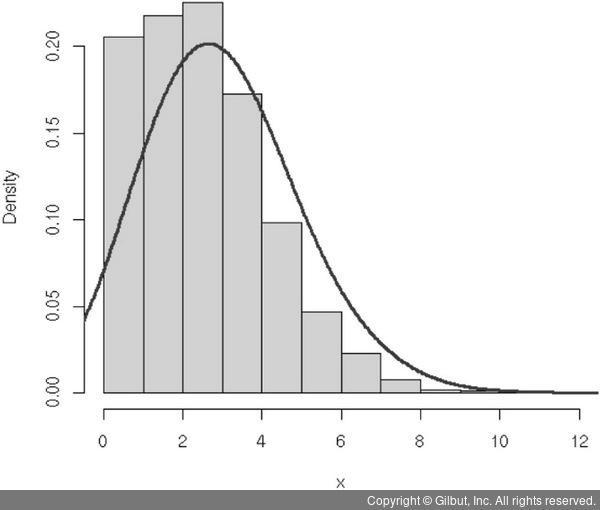
포아송 회귀모형은 정규방정식(OLS, Ordinary Least Square)과는 다른 추정 방법을 사용하기에 로그 선형모형(loglinear model)이라고도 불린다. 이 모형에서는 변수 Y가 포아송 분포를 따르는 것을 가정하며 이때 종속 변수는 특정 지역, 개인에게서 특정 사건의 빈도에 대한 데이터이기 때문에 음수는 나오지 않는다. Y값의 분포가 그림 7-8과 같이 좌측으로 쏠려 있다면 포아송 회귀모형을 적용하는 것을 고려한다.

▲ 그림 7-8 사건 발생 횟수(count data)의 분포