하지만 포아송 회귀모형도 역시 회귀모형이기 때문에 X와 Y의 관계를 식으로 나타내고자 한다. 이때 X와 Y의 관계가 비선형이기 때문에 직선식으로 나타내려면 X와 Y의 관계를 선형 관계로 변환해야 한다. 이런 경우 우리는 Y를 변환하는데, Y에 로그(log) 함수를 적용한다. log(Y)는 X와 선형 관계를 갖게 되면서 직선식으로 나타낼 수 있다. 이때 Y에 적용하는 로그 함수를 연결(link) 함수라고 부른다. 이렇게 변형된 Y에 대해 X로 직선식을 구하면 다음과 같은 형태의 결과를 얻을 수 있다.
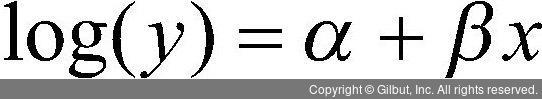
그럼 선형 회귀모형 직선식의 기울기와 포아송 회귀모형 직선식의 기울기는 어떻게 다를까? 다음의 포아송 회귀 모형을 예로 들어보자.
log(y) = 0.2x1 - 1.1x2 - 0.4x3 - 0.05x4 + 0.05x5 + 1
앞의 모형에 대해서 각 X의 값이 (x1, x2, x3, x4, x5) = (1, 0, 0, 1, 0)으로 주어졌다면 log(y)의 값은 1.15로 예측된다. 실제 구하려는 값은 y기 때문에 log(y) = 1.15의 양변에 지수를 적용한다. 지수를 적용하면 exp(log(y))는 y가 되어 좌변이 정리되고, 우변은 exp(1.15)가 된다. 즉, 예측되는 y값은 exp(1.15) = 3.158이 된다.
포아송 회귀모형의 모형 적합도는 편차(deviance)나 아카이케 정보 기준(AIC, Akaike Information Criteria)을 사용하고, 이 값들이 작을수록 모형은 좋다고 고려한다. 그리고 모형에 X가 한 개도 없을 때 구한 편차 값과 모형에 X를 넣어 구한 편차 값의 차이를 통해 X가 Y를 얼마나 잘 설명하는지를 살펴본다. 즉, 특정한 독립 변수를 포함한 모형의 편차와 포함하지 않은 모형의 편차를 비교한 후 p값으로 변수를 추가한 유의성을 볼 수 있다.
포아송 회귀모형은 Y의 과분포(overdispersion) 이슈가 있다. 즉, 포아송 분포는 평균과 분산이 같다는 특징이 있는데, 이 가정을 만족시키지 않고 Y의 분산이 평균보다 큰 경우에는 과분포가 발생한다. 이 경우 계수는 동일하게 계산된다 하더라도 표준편차가 변하여 검정 통계량 및 p값도 영향을 받으며, 계수에 대한 해석도 영향을 받을 수 있어 어렵게 구한 모형을 활용하지 못할 수도 있다. 이런 문제가 발생할 때는 포아송 분포의 조건을 일부 완화한 준포아송(quasi-poisson) 확률 분포를 사용하여 포아송 회귀모형을 만들기도 한다.