이때 양변에 지수(exponential)를 취해주고 p를 좌변으로, 나머지를 우변으로 정리하면 다음 식이 나온다.

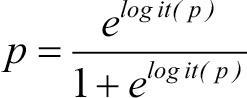
이때 logit(p) 부분에 앞에서 x 항으로 표현한 식을 대입하면 p는 다음과 같이 x 항과 계수에 의해 표현할 수 있다. 즉, x에 해당하는 데이터와 모형에서 추정된 계수들이 있다면 p값을 계산할 수 있는 셈이다!

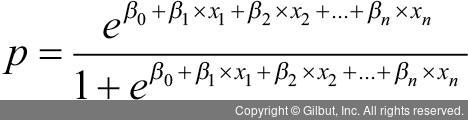
그렇다면 로지스틱 회귀모형에서 독립 변수인 X의 계수들은 어떻게 추정할 수 있을까? 잔차들의 정규성과 등분산성을 가정하는 선형 회귀모형처럼 원래 Y값과 예측한 Y값의 차이를 통해 계산된 잔차제곱합(Sum of Squared Errors)를 최소화하는 계수 추정 방법은 적절하지 않다(Y는 범주이기 때문에 뺄셈이 안 된다). 결론부터 얘기하면 로지스틱 회귀모형은 최대 우도 추정(maximum likelihood estimation)이라는 새로운 방법을 통해 계수를 추정하는데, 이 추정된 계수는 예측한 Y를 실제 Y와 최대한 같게 만든다. 이 추정 과정은 반복적인 시행착오(trial and error)로 진행되며, 계산된 계수는 지수의 계수 승만큼 Y에 영향을 준다고 해석할 수 있다.

이러한 로지스틱 회귀모형의 적합도(goodness of fit)는 편차 값을 통해서 살펴볼 수 있다. 즉, 모형의 편차가 작을수록 모형의 적합이 좋다고 볼 수 있다. 주로 특정 독립 변수를 포함한 모형의 편차와 포함하지 않은 모형의 편차를 비교하여, 각 경우 p값을 비교하여 변수 추가의 유의성을 보기도 한다. 즉, 주어진 영모형에서의 편차(null deviance)와 잔차의 편차(residual deviance)를 비교하고 이 차이를 다른 모형의 편차 차이와 비교하여 작은 쪽이 좋은 모형이 된다. 그러나 무작정 독립 변수를 계속 추가하면 편차는 작아지는 성질이 있으므로 주의가 필요하다.