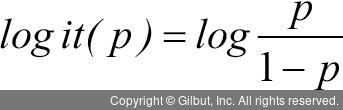4. 선형 회귀 분석을 통한 예측

• 추정한 모형에 예측하려는 X를 넣어서 Y를 예측한다.
• 예를 들어 X 변수 하나가 포함된 추정 모형이 Y = 5 × X + 10이고, 예측하려는 X가 10이면 예측값 Y = 5 × 10 + 10이어서 60으로 계산된다.
• 예측한 Y와 실제 Y의 차이는 오차이다.
• 예측한 값들이 갖는 오차 값의 제곱의 평균은 평균오차제곱(MSE, Mean Squared Error)이다.

5. 분류모형(classification)

• 범주형 Y 변수에 대해 모형화하는 것이다.
• Y가 갖는 범주를 예측할 수 있다.
• Y 변수가 사고의 발생/미발생, Yes/No와 같은 이항 분포를 따르는 경우에 적용할 수 있다.

6. 로지스틱 회귀(logistic regression) 분석

• 주어진 X로 Y의 범주를 예측하는 분석이다.
• X는 독립 변수, Y는 종속 변수라고 지칭한다.
• 로지스틱 회귀 분석을 통해 X가 Y의 발생에 미치는 관계를 추론할 수 있다.
• 다음 식으로 표현한다.

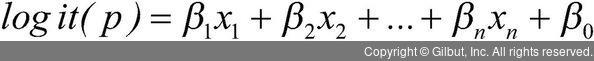
• 이때 logit(p)에서 p는 대상 사건이 발생할 확률이며 아래 식으로 표현한다.